Meist reicht ein Lageparameter als Zusammenfassung einer Datenreihe nicht aus, und man wünscht sich mehr Information. Streuungsparameter sind nun ein Maß dafür, wie sehr die Daten um einen Mittelwert schwanken. Auch hier gibt es verschiedene Möglichkeiten, solche Kennziffern zu berechnen. In der Praxis wird allerdings meist die Varianz bzw. ihre Wurzel, die Standardabweichung benutzt.
Da (zumindest die gebräuchlichen) Streuungsparameter in ihrer Definition immer irgendwo eine Differenz beinhalten, kann man sie nur für numerische Daten bestimmen, also diskrete oder stetige Zahlen. Bei einem nominal- oder ordinalskalierten Merkmal ist das nicht möglich.
Das Wichtigste in Kürze
Für gemessene Daten \(x_1, x_2, \ldots, x_n\):
- Spannweite:
- \[ x_\text{max} – x_\text{min} \]
- Interquartilsabstand:
- \[ x_{0.75} – x_{0.25} \]
- Varianz:
-
- In einer Stichprobe (meistens der Fall) kann man die folgenden zwei äquivalenten Formeln verwenden:
\[ \begin{align*} s^2 & = \frac{1}{n-1} \sum_{i=1}^n (x_i-\bar{x})^2 \\ s^2 & = \left( \frac{1}{n-1}\sum_{i=1}^n x_i^2 \right)-\frac{n}{n-1}\bar{x}^2\end{align*}\] - In einer Vollerhebung oder wenn der wahre Mittelwert \(\mu\) bekannt ist (selten der Fall) verwendet man eine dieser beiden Formeln:
\[ \begin{align*} \tilde{s}^2 & = \frac{1}{n} \sum_{i=1}^n (x_i-\mu)^2 \\ \tilde{s}^2 &= \left( \frac{1}{n}\sum_{i=1}^n x_i^2 \right)-\mu^2 \end{align*} \]
- In einer Stichprobe (meistens der Fall) kann man die folgenden zwei äquivalenten Formeln verwenden:
- Standardabweichung:
-
- In einer Stichprobe: \(s = \sqrt{s^2}\)
- In einer Vollerhebung oder bei bekanntem Mittelwert: \(\tilde{s} = \sqrt{\tilde{s}^2}\)
Spannweite und Quartilsabstand
Die Spannweite einer Datenreihe ist definiert als der Abstand zwischen dem
Maximum und dem Minimum dieser Daten:
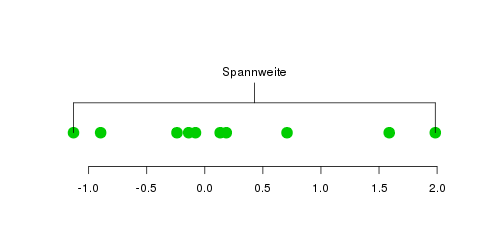
Man sucht also in den Daten nach dem Maximum und dem Minimum, und zieht das Minimum vom Maximum ab—so erhält man die Spannweite. Das ist ein sehr einfaches Streuungsmaß, aber unglaublich anfällig für Ausreißer (was in der Statistik meist unerwünscht ist). Daher betrachtet man auch den Interquartilsabstand, der ein bisschen dagegen hilft; er ist der Abstand zwischen dem 75%-Quantil und dem 25%-Quantil:
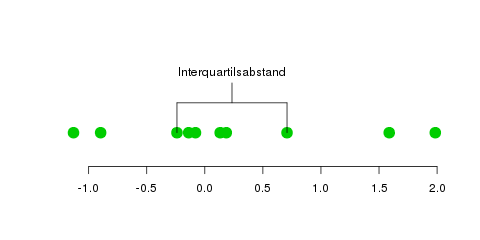
Hier muss man also das 75%-Quantil (\(x_{0.75}\)) und das 25%-Quantil (\(x_{0.25}\)) berechnen, und erhält den Interquartilsabstand durch \( x_{0.75}-x_{0.25} \). Im oberen Bild mit \(n=10\) Datenpunkten ist das 25%-Quantil bestimmt als \(x_{0.25}=x_{(\lfloor np \rfloor + 1)} = x_{(3)}\), und das 75%-Quantil analog als \(x_{(8)}\). Die tatsächlichen Werte der Datenpunkte sind hier nicht berücksichtigt, aber wir nehmen immer den dritten und achten Wert der sortierten Daten.
Den Interquartilsabstand interessiert es nun nicht, ob die „äußeren“ Daten (also \(x_{(1)}\), \(x_{(2)}\), \(x_{(9)}\) und \(x_{(10)}\)) Ausreißer sind oder nicht, also wenn man sie weiter nach aussen verschieben würde.
Varianz und Standardabweichung
Für die Varianz einer Reihe von Daten gibt es dummerweise zwei ähnliche, aber verschiedene Formeln. Zu allem Übel gibt es für die beiden Formeln keine einheitliche Bezeichnung. Welche man verwendet, hängt von der Art der Daten ab, die man ansieht.
Die Idee hinter der Varianz ist grob ausgedrückt die folgende: Man will wissen, wie weit die Daten \((x_1, x_2, \ldots, x_n)\) normalerweise vom Mittelwert \(\mu\) abweichen—das ist die Distanz \((x_i-\mu)\). Dabei ist egal, ob die Abweichung nach oben oder nach unten ist, daher quadriert man die Distanz (Man könnte hier natürlich auch den Betrag der Distanz statt dem Quadrat nehmen. Allerdings macht es später vieles einfacher, wenn wir das Quadrat nehmen, z.B. die Maximum-Likelihood-Schätzung oder die Regression. So gesehen ist es rein willkürlich, dass man den quadratischen Abstand verwendet.): \((x_i-\mu)^2\). Und genau aus diesem quadratischen Abstand wird nun der Mittelwert über alle Daten, d.h. alle \(x_i\) gebildet: \(\frac{1}{n} \sum_{i=1}^n (x_i-\mu)^2\).
Ist der wahre Mittelwert der Daten bekannt, benutzt man die empirische Varianz, \(\tilde{s}^2\). Wenn die Daten die komplette Grundgesamtheit widerspiegeln, ist dies der Fall, da man den wahren Mittelwert ja ausrechnen kann, wenn einem alle Daten zur Verfügung stehen. Die empirische Varianz ist für eine Datenreihe \(x_1, x_2, \ldots, x_n\) und deren Mittelwert \(\mu\) folgendermaßen bestimmt:
\[ \tilde{s}^2 = \frac{1}{n} \sum_{i=1}^n (x_i-\mu)^2 \]
Meistens ist der wahre Mittelwert der unterliegenden Grundgesamtheit allerdings nicht bekannt, und man benutzt stattdessen den Mittelwert der Stichprobe (Vorsicht: Das sind zwei verschiedene Dinge: Der wahre Mittelwert ist ein fester Wert und ändert sich innerhalb der Grundgesamtheit nie, aber das Stichprobenmittel ist im Allgemeinen für jede Stichprobe ein anderer). Man bestimmt also, wie sehr die Daten um das Stichprobenmittel streuen, und nicht, wie stark sie um den wahren Mittelwert streuen. In diesem Fall, der eigentlich so gut wie immer gegeben ist, betrachtet man die (korrigierte) Stichprobenvarianz \(s^2\), die folgendermaßen bestimmt ist:
\[ s^2 = \frac{1}{n-1} \sum_{i=1}^n (x_i-\bar{x})^2 \]
Der Unterschied zu der empirischen Varianz \(\tilde{s}^2\) ist, dass in der Summe jeweils das Stichprobenmittel \(\bar{x}\) abgezogen wird, und dass vor der Summe durch \(n-1\) statt \(n\) geteilt wird. Für größere Stichproben wird der Unterschied zwischen \(s^2\) und \(\tilde{s}^2\) immer kleiner, da für sehr grosse \(n\) erstens der Unterschied zwischen \(n\) und \(n-1\) nicht mehr so wichtig ist, und zum anderen das Stichprobenmittel \(\bar{x}\) immer näher an den wahren Mittelwert \(\mu\) der Grundgesamtheit kommt (Der Grund für dieses Verhalten ist das Gesetz der großen Zahlen, das wir uns später noch anschauen werden).
Die Berechnung der Varianz mit dem Taschenrechner ist ziemlich nervig. Als kleine Hilfestellung dafür gibt es den sogenannten Verschiebungssatz. Nach ihm kann man die Formel der empirischen bzw. Stichproben-Varianz folgendermaßen umschreiben:
\[ \begin{array}{rclcl} \tilde{s}^2 & = & \frac{1}{n} \sum_{i=1}^n (x_i-\mu)^2 & = & \left( \frac{1}{n}\sum_{i=1}^n x_i^2 \right)-\mu^2 \\ s^2 & = & \frac{1}{n-1} \sum_{i=1}^n (x_i-\bar{x})^2 & = & \left( \frac{1}{n-1}\sum_{i=1}^n x_i^2 \right)-\frac{n}{n-1}\bar{x}^2 \end{array} \]
Die jeweils rechte Seite der Gleichung ist nun die neue Formel. Sie ist bei der Berechnung von Hand angenehmer, weil man nicht erst den Mittelwert ausrechnen muss. Außerdem hat die zweite Formel den Vorteil, dass sie nicht nochmal komplett von vorne berechnet werden muss, wenn ein neuer Datenpunkt zu den Daten dazukommt. Man kann dann nämlich zur gesamten Summe der \(x_i\) und \(x_i^2\) den neuen Wert einfach addieren, und \(n\) um eins erhöhen. In der alten Formel müsste man jede Teilsumme \((x_i-\bar{x})^2\) nochmal ausrechnen, da sich ja durch den neuen Datenpunkt das Stichprobenmittel \(\bar{x}\) bzw. der Erwartungswert \(\mu\) verändert hat.
Die Standardabweichung einer Datenreihe ist einfach die Wurzel aus der Varianz. Je nachdem, welche Formel man für die Varianz verwendet hat (wie gesagt, meistens ist es die Stichprobenvarianz, die durch \(n-1\) teilt), ist die Standardabweichung \(s\) entweder \(\sqrt{s^2}\) oder \(\sqrt{\tilde{s}^2}\).
Beispielaufgabe
Schauen wir uns Beispieldaten eines diskreten Merkmals für 7 Personen an. Wir berechnen für diese Datenreihe die Spannweite, den Interquartilsabstand, und die Varianz und Standardabweichung.
| Person | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Merkmal | 3 | 2 | 0 | 5 | 1 | 4 | 4 |
Für Spannweite und Interquartilsabstand brauchen wir zuerst wieder die sortierten Daten:
| geordnetes Merkmal | 0 | 1 | 2 | 3 | 4 | 4 | 5 |
|---|
Die Spannweite ist also \(5-0=5\).
Für den Interquartilsabstand berechnen wir zuerst
- \(x_{(0.25)} = x_{(\lfloor np \rfloor +1)} = x_{(\lfloor 7\cdot 0.25 \rfloor +1)} = x_{(2)} = 1\) und
- \(x_{(0.75)} = x_{(\lfloor np \rfloor +1)}= x_{(\lfloor 7\cdot 0.75 \rfloor +1)} = x_{(6)} = 4\).
(Die Klammern \(\lfloor\) und \(\rfloor\) bedeuten hier Abrunden)
Der Interquartilsabstand ist nun \(x_{0.75}-x_{0.25}=4-1=3\).
Die Varianz geht ein bisschen mühsamer, aber einfach nach Formel. Nachdem wir den Mittelwert \(\bar{x}=2.714\) berechnet haben:
\[ \begin{align*} s^2 = & \frac{1}{n-1} \sum_{i=1}^n (x_i-\bar{x})^2 \\ = &\frac{1}{6} \cdot [ (3-2.714)^2 + (2-2.714)^2 + (0-2.714)^2 + \\ & (5-2.714)^2 + (1-2.714)^2 + (4-2.714)^2 + (4-2.714)^2 ] \\ =& 3.238 \end{align*} \]
Die Standardabweichung ist nun einfach \(\sqrt{s^2} = \sqrt{3.238} = 1.799\).

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Hallo,
ich habe eine Frage.
Kann man zur Berechnung der Varianz folgende Formel verwenden?
V(x)= P(Xi) * (E(x) – Xi)^2 + …
Verstehe das hier dargestellte leider nicht so ganz
Liebe Grüße
Hi, du verwechselst die Stichprobenvarianz (von erhobenen Daten) mit der Varianz einer Zufallsvariablen. Ich glaube du suchst diesen Artikel hier: https://www.crashkurs-statistik.de/darstellung-und-eigenschaften-von-diskreten-zufallsvariablen/#varianz
Ich versuche den Einfluss von “skill” beim Poker auf die Varianz zu betrachten. Einfluss auf die Varianz beim Pokern haben Faktoren wie Spielstil, buyin Strategie, Anzahl der Spieler, Setzverhalten der Gegner, Konditionen des Anbieters (Gebühren) etc. Ein Spieler mit mehr Können hat einen höheren Erwartungswert als ein schlechterer Spieler. Der Durchschnitt ist also höher. Bei einem Varianzkalkulator (pokerdope.com) als auch bei der empirischen Auswertung meiner Daten (n=3000), ist auffällig, dass die Glocke um den Erwartungswert schmaler wird. Je schmaler die Glocke, desto geringer die Varianz?!? Bei der Berechnung kommt ebenfalls ein kleinerer Wert für die Varianz heraus bei größerem Skillfaktor. Meine Frage nun: Wie beeinflusst der Durchschnitt die Varianz?
Moin,
ich hätte eine Frage zur Varianz. Wenn ich bei einer Verteilung nur den unteren Teil betrachten möchte, dann beziehe ich für X nur die Werte ein, die den Mittelwert der gesamten Verteilung unterschreiten.
Die Frage ist nun, ob ich bei der Berechnung dann für n die Anzahl der gesamten Beobachtungen einsetze, oder nur die Anzahl der negativen Beobachtungen.
Gruß
Deine Stichprobe sind dann nur die negativen Beobachtungen, also ist n dann nur deren Anzahl.
VG
Alex
Gibt es einen Unterschied zwischen „wahrer Mittelwert“ und Erwartungswert?
Nein, das ist dasselbe
Hey! Muss die Stichprobe normalverteilt sein um die Streuung als Standartabweichung anzugeben? Ich habe einige Publikationen gesehen, die keine normalverteilte Stichprobe haben und dann mit den Interquantil Ranges arbeiten. Habe ich das richtig verstanden? Vielen Dank!!
Sie muss nicht, nein. Da gibt es keine Regeln dafür, welches Maß man verwendet, eher übliche Praktiken. Die IQR bietet sich bei schiefen Verteilungen an.
Bei der Beispielaufgabe habe ich eine Frage und zwar bei den Interquartilsabständen x(0,25)= ((7*0,25)+1) wieso kommt man da auf 2? Ich komme da auf 2,75 – ist das nicht aufgerundet dann 3? Oder rundet man hier in diesem Fall immer ab? Sorry für diese doofe Frage.
Die Klammern \(\lfloor\) und \(\rfloor\) bedeuten, dass man immer abrundet, ja. Das ist in diesem Artikel unten nochmal erklärt:
http://www.crashkurs-statistik.de/quantile/
Hallo,
zuerst: Super machst du das! Schreibe bald meine Statisikklausur und deine Seite hilft mir sehr gut! Alles wunderbar erklärt 🙂
Ich habe jedoch eine Frage, in der Beispielaufgabe hast du die Formel für die Stichprobe genommen -> müsste hier nicht eigentlich nur durch n geteilt werden? Die Grundgesamtheit ist ja bekannt und wir berechnen vorab den Mittelwert (wie bei der Formel für den wahren Mittelwert) oder handelt es sich um eine Stichprobe und den Hinweis hierzu übersehe ich?
Vielen Dank schon mal
Ja, es ist eine Stichprobe. Explizit wurde das nirgends erwähnt, aber davon kann man meistens ausgehen 🙂
wow deine arbeit ist der hammer, meine statistik klausur steht bald in 1,5 monaten an und hier finde ich so ziemlich alles was ich brauche sehr schön erklärt. hier werden viele fragen gezielt beantwortet, für die mein Prof erstmal 10 minuten ausholen muss. danke sehr. Bitte mach weiter so!
lg ein Fan!
Danke auch :3
Vielen Dank für Ihren Blog, er hilft mir gerade sehr dabei mich wieder in die Wahrscheinlichkeitstheorie einzuarbeiten. Das war jetzt auch der erste Artikel im Netz, wo mal geschrieben wurde, dass das Quadrieren bei der Varianzberechnung eher willkürlich ist und dass man auch den Betrag hätte nehmen können. Das hatte ich mich schon öfter gefragt 🙂
Was mir leider noch fehlt, ist eine mathematisch präzisere Erklärung, weshalb es sinnvoll ist, bei Stichproben durch (n-1) statt durch n zu teilen. Geht das in irgendwelche Konvergenzberechnungen ein oder gibt es sonst einen Beweis oder eine gute Erklärung, weshalb man gerade „nur“ 1 abzieht?
Danke und viele Grüße von einem Mathematikerkollegen
Hi Paul,
es gibt einen Unterschied zwischen der empirischen Varianz und der Stichprobenvarianz. Bei der empirischen Varianz teilt man tatsächlich durch \(\frac{1}{n}\), das ist dann genau die „durchschnittliche quadratische Abweichung vom Mittelwert“.
Wenn man aber eine Stichprobe hat, muss man den Mittelwert schätzen. Man hat also nicht \(\mu\), den echten Mittelwert, sondern \(\bar{x}\), den geschätzten. Dadurch verliert man einen ‚Freiheitsgrad‘, und den zieht man im Nenner wieder ab.
Das mit den Freiheitsgraden ist ziemlich seltsam, und ich hab es selbst noch nicht zu 100% verstanden. Aber stell dir vor der wahre Mittelwert ist bekannt als \(\mu=6\) und du ziehst eine Stichprobe von einem einzigen Datenpunkt, der dann \(x=5\) ist. Die Varianz wird dann 1 sein.
Wenn der Mittelwert aber unbekannt ist, und du ziehst eine Stichprobe von \(x=3\), musst du den Mittelwert zu \(\bar{x}=3\) schätzen. Jetzt wäre die Varianz aber gleich 0, aber nicht weil der Datenpunkt genau den tatsächlichen Mittelwert \(\mu\) getroffen hat, sondern weil du ihn genau auf 3 geschätzt hast.
Das ist ziemlich schwer zu erklären merke ich gerade. Ich hoffe aber es hat ein wenig geholfen 🙂
Viele Grüße,
Alex
Hi Alex,
vielen Dank für die schnelle Antwort!
Ich werde darüber nachdenken und mal mit meinem Chef (Prof) drüber sprechen. Sollte ich etwas erhellendes dabei erfahren, werde ich es schreiben.
Viele Grüße
Hi,
ich hab grad die Lösung gefunden:
Der Schätzer soll ja bitte auch erwartungstreu sein, also muss der Erwartungswert der geschätzen Varianz gleich der Varianz sein. Die Herleitung des 1/(n-1) Faktors findet man hier:
https://de.wikipedia.org/wiki/Korrigierte_Stichprobenvarianz
Damit ist das auch geklärt 🙂
Viele Grüße
Ich habe folgende Frage:
Wenn ich nur Minimum und Maximum angegeben habe, kann ich dann auch den Mittelwert darüber berechnen?
Nein, du brauchst jeden Messpunkt.
Hi, mir wird nicht klar wieso die Spannweite ausreißerabhängig ist und der Qurtilsabstand nicht. LG
Ich bin mal so frei und antworte hier.
Die Spannweite ist ausreißerabhängig, weil in ihr ja wirklich alle Messwerte eingehen. Angenommen in einer Schulklasse sind alle Schüler zwischen 1,70 und 1,80 m groß, dann ist die Spannweite nur 10cm. Nun kommen zum neuen Jahr aber ein Riese (2m) und eine sehr kleine Schülerin (1,50) dazu. Und schon ist die Spannweite verfünffacht, nämlich zu 50 cm. Aber diese Zahl täuscht einem nur vor, dass in dieser Klasse die Leute sehr unterschiedlich groß sind, obwohl eigentlich (fast) alle recht ähnlich groß sind.
Nimmt man aber nur die „inneren 75%“, so machen der Riese und die kleine Schülerin (also die Ausreißer der Daten) nichts aus, da sie nicht zur breiten Masse gehören.
Hey,
ich glaube es müsste nur 1/n, nicht 1/(n-1) bei der Formel für die Varianz sein. 🙂
Hi Alicia,
das kommt drauf an, ob man die Stichprobenvarianz ( \(\frac{1}{n-1}\) ) oder die empirische Varianz ( \(\frac{1}{n}\) ) berechnet. Die beiden Formeln sind ganz oben im Artikel erwähnt, und wann man welche verwendet. Meistens wird durch \(n-1\) geteilt 🙂
Gruß,
Alex
ich komme komischerweise nicht auf die Varianz aus der Klausuraufgabe!
hat sich erledigt! 😀
Hi,
vielen Dank. Stimmte alles, ich habs übernommen. 🙂
Hallo,
in der Beispielaufgabe soll es bei der Berechnung vom Interquartilsabstand x0.75−x0.25=4−1=3 stehen, oder? Da x0.25 gleich 1 ist.
In der Klausuraufgabe kommt bei mir der Wert 8.637 für die Varianz heraus.
P.S. Im Abschnitt „Varianz und Standardabweichung“ im 2. Absatz ist ein Tippfehler drin („Regrssion“).