Die diskrete Gleichverteilung liegt vor, wenn eine Zufallsvariable
- diskret ist, also das Experiment nur eine endliche Zahl an möglichen Ergebnissen hat, und
- jedes mögliche Ergebnis mit derselben Wahrscheinlichkeit auftritt.
Zwei schöne Beispiele hierfür sind der Münzwurf mit \(n=2\) möglichen Ergebnissen, Kopf oder Zahl, wo jedes mit der gleichen Wahrscheinlichkeit, \(\frac{1}{2}\), auftritt, und das Rouletterad mit \(n=37\) möglichen Ergebnissen (der Null und die Zahlen 1 bis 36), wo jede Zahl mit der Wahrscheinlichkeit \(\frac{1}{37}\) auftritt.
Parameter
Die möglichen Ergebnisse werden bezeichnet mit den Variablen \(x_1, x_2, \ldots, x_n\). Für das Beispiel des Münzwurfs können wir also „Kopf“ mit 1 kodieren, und „Zahl“ mit 2, und erhalten die möglichen Ergebnisse \(x_1=1, x_2=2\) (wir müssen diese Ereignisse in Zahlen umwandeln, der Grund ist im Artikel Was sind Zufallsvariablen? ganz oben erklärt.). Für das Roulette-Beispiel erhalten wir \(x_1=0, x_2=1, x_3=2, \ldots, x_{37}=36\).
Wir beschränken uns hier aber auf einen Spezialfall, nämlich Zufallsexperimente, deren Ergebnis jede Ganzzahl zwischen \(a\) und \(b\) sein kann. Beim Münzwurf haben wir also eine Gleichverteilung mit den zwei Parametern \(a=1\) und \(b=2\), und beim Roulettespiel eine Gleichverteilung mit \(a=0\) und \(b=36\). Mit dieser Art der Modellierung können wir die allermeisten Situationen modellieren, bis auf manche Sonderfälle, zum Beispiel das Punkteergebnis eines Fußballspiels, in dem ein Verein entweder 0, 1, oder 3 Punkte bekommt.
Träger
Der Träger \(\mathcal{T}\) der diskreten Gleichverteilung sind die einzelnen Ausprägungen \({x_1, x_2, \ldots, x_n}\), also alle ganzen Zahlen zwischen \(a\) und \(b\). Beim Roulettespiel sind das z.B. die Zahlen \({0, 1, 2, \ldots, 36}\). Andere Ergebnisse sind in diesem Beispiel nicht möglich: Das Rouletterad kann zum Beispiel keine 52, oder keine 3,5 zeigen.
Dichte
Die Dichtefunktion muss in zwei Teile aufgeteilt werden. Beim Roulettespiel ist z.B. die Wahrscheinlichkeit, dass die 17 erscheint, \(\mathbb{P}(X=17) = \frac{1}{37}\), aber die Wahrscheinlichkeit, dass das Ergebnis 1500 ist, \(\mathbb{P}(X=1500) = 0\). Die Dichte für das Roulettespiel ist also
\[ f(x) = \begin{cases} \frac{1}{37}, & x \in \{0, 1, \ldots , 36\} \\ 0, & \text{sonst} \end{cases} \]
Im Allgemeinen haben wir \(n\) verschiedene Ergebnisse für eine Zufallsvariable, die wir mit \(x_1, x_2, \ldots, x_n\) bezeichnen (also wieder alle Zahlen von \(a\) bis \(b\), den Träger). Hier ist die Dichte dann
\[ f(x) = \begin{cases} \frac{1}{n}, & x \in \{ a, a+1, \ldots , b \} \\ 0, & \text{sonst} \end{cases} \]
Verteilungsfunktion
Die Verteilungsfunktion der diskreten Gleichverteilung lautet wie folgt:
\[ F(x) = \begin{cases} 0, & x < a \\ \frac{\lfloor x \rfloor – a + 1}{b-a+1}, & x \in [a,b]\\ 1, & x > b \end{cases}\]
„Links“ von \(a\) ist die Verteilungsfunktion also immer 0, und „rechts“ von \(b\) ist sie immer 1. Mit \(\lfloor x \rfloor\) ist hier die Abrundung von \(x\) gemeint, also ist z.B. \(\lfloor 3.4 \rfloor = 3\) und \(\lfloor 5 \rfloor = 5\).
Möchten wir für das Roulettespiel z.B. bestimmen, mit welcher Wahrscheinlichkeit eine Zahl kleiner oder gleich 3.5 kommt, bestimmen wir:
\[ F(3.5) = \frac{\lfloor 3.5 \rfloor – 0 + 1}{36 – 0 + 1} = \frac{4}{37} \]
Versuche, mit dieser Definition für das Beispiel Würfelwurf zu bestimmen:
- \(F(4)\), also die Wahrscheinlichkeit, mit der wir eine Augenzahl würfeln, die kleiner oder gleich 4 ist.
- \(F(4.8)\)
- \(F(0)\)
- \(F(1500)\)
Erwartungswert
Der Erwartungswert ist bei der diskreten Gleichverteilung einfach der Mittelwert von \(a\) und \(b\):
\[ \mathbb{E}(X) = \frac{a+b}{2} \]
Varianz
Die Varianz dieser Verteilung lautet:
\[ \mathbb{V}(X) = \frac{(b-a+1)^2 – 1}{12} \]
Beispielaufgabe
Schauen wir uns die Zufallsvariable „\(X\) = ein Würfelwurf“ an, und bestimmen für sie
- Träger
- Dichte
- Verteilungsfunktion
- Erwartungswert
- Varianz
Träger
Die Zufallsvariable \(X\) kann nur die Werte 1, 2, 3, 4, 5, oder 6 annehmen. Also ist der Träger \(\{ 1, 2, 3, 4, 5, 6 \}\).
Dichte
Die Dichte ist, wenn wir die obige Definition anwenden, einfach bestimmt:
\[ f(x) = \begin{cases} \frac{1}{6}, & x \in \{ 1, 2, 3, 4, 5, 6 \} \\ 0, & \text{sonst} \end{cases} \]
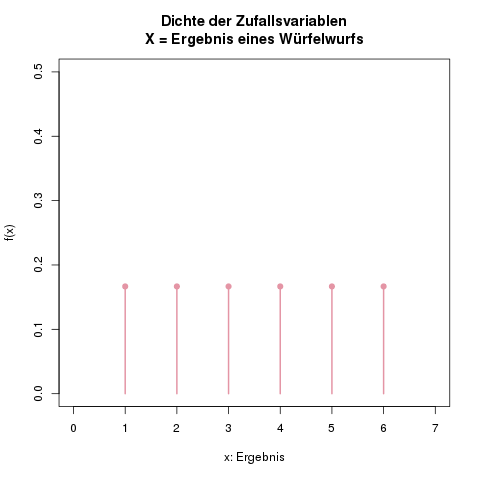
Dichte der diskreten Gleichverteilung beim Experiment „Werfen eines Würfels“. Jedes Ereignis von 1 bis 6 tritt mit der gleichen Wahrscheinlichkeit \(\mathbb{P}(X=i) = \frac{1}{6}\) auf.
Verteilungsfunktion
Die Verteilungsfunktion ist einfach notierbar als:
\[ F(x) =\begin{cases}0, & x < 1\\ \frac{\lfloor x \rfloor}{6},& 1 \leq x <6\\ 1, & x \geq 6 \end{cases}\]
Erwartungswert
Der Erwartungswert eines Würfelwurfs ist
\[ \mathbb{E}(X) = \frac{1}{2} (6 + 1) = 3.5 \]
Varianz
Auch hier sind wir schnell am Ziel. Die Formel angewendet lautet
\[ \mathbb{V}(X) = \frac{(6-1+1)^2 – 1}{12} = 2.917 \]

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!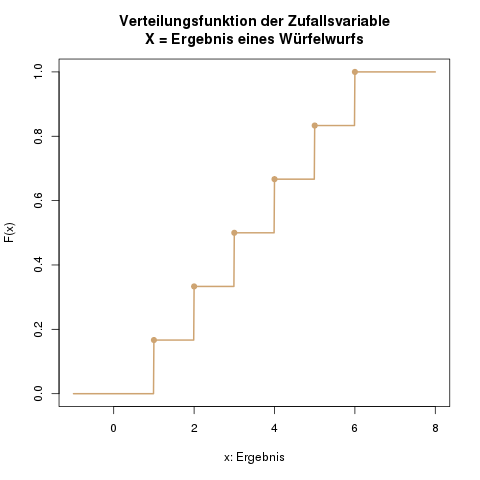
Hallo Alex,
ich bin noch weit weg vom verstehen, kämpfe mich aber durch. Frage: müßte beim Würfelbeispiel beim dritten Abschnitt der Verteilungsfunktion nicht „größer 6“ statt „größer gleich 6“ stehen?
Gruß, Susanne
Hallo Susanne,
das „größer gleich 6“ stimmt schon so. Falls x nämlich genau gleich 6 ist, dann bedeutet das F(6), was wiederum in Worten bedeutet: „Die Wahrscheinlichkeit, dass x kleiner oder gleich 6 ist.“
Und der Würfel zeigt mit einer Wahrscheinlichkeit von 1 (also 100%) eine Zahl kleiner oder gleich 6.
Ich hoffe das ist einigermaßen verständlich 🙂
Viele Grüße
Alex
Hallo,
Ich habe eine Frage und zwar sind die hier benutzten Formeln nicht die für die stetige Gleichverteilung?
Zum Bsp: E(X) etc..?
Hi,
manche Formeln sind in der stetigen und diskreten Gleichverteilung dieselben. Hier z.B. der Erwartungswert. Das gilt aber nur in dem Spezialfall der diskreten Gleichverteilung, wenn alle Ganzzahlen zwischen \(a\) und \(b\) betrachtet werden (ist im zweiten Absatz hier erklärt).
Die Varianz ist z.B. minimal anders definiert, das kannst du im Artikel zur stetigen Gleichverteilung nachprüfen.
Ah okay danke,
Habe auf der Formelsammlung irgendwie komische Formeln für die diskrete Gleichverteilung.
Ich hoffe einfach dass entweder so ein Beispiel für diskrete dran kommt oder eines für stetige
Vielen Dank für den Artikel 🙂
Ich meine aber, die Varianzformel lautet nicht (b-a+1)^2-1/12, sondern (b-a+2)(b-a)/12 oder?
Und wieso fehlt im Würfelrechenbeispiel dann die -1 im Zähler? Hmm. Bin verwirrt.
Oh, mein Fehler. Ist korrigiert, vielen Dank!
Super, ich danke dir 🙂 dann hab ichs nun kapiert!
Hallo Alex,
Jetzt ist mir das Thema klarer geworden. Ich habe nur eine Frage, wer ist die Author von die Verteilungsfunktion die du hier darstellst?
⌊x⌋−a+1b−a+1 Ich habe besonders Fragen wegen ⌊x⌋ ?
Danke !
Hallo,
der Autor bin ich 🙂
Zu der Funktion findest du hier eine kurze Erklärung:
http://www.crashkurs-statistik.de/mathematische-symbole/
Vielleicht reicht das schon.
Viele Grüße,
Alex
Das müsste dasselbe sein, also die eine Darstellung lässt sich zur anderen umformen. Beide Formeln sind korrekt 🙂
Achso! Im Umformen war ich schon immer mies. Dankeschön =)!
Ich komme nicht auf die Lösung deiner Aufgabe unter „Verteilungsfunktion“.
Laut der vereinfachten Darstellung ergibt F(1500)=1 , da 1500>6 sprich wir würfeln zu 100% eine 1500???
Wär super wenn du mir den richtigen Lösungsansatz erklären könntest 🙂
Ne, wir würfeln zu 100% eine Zahl kleiner oder gleich 1500.
Die Dichte würde die Wahrscheinlichkeit berechnen, genau eine 1500 zu würfeln – das wäre natürich 0.
Okok aber „kleiner gleich“ beinhaltet doch immerhin auch die Möglichkeit eine 1500 zu würfeln was ja kaum möglich sein dürfte^^
Vll steh ich auch nur komplett aufm Schlauch?
Kleiner gleich beinhaltet auch die Ergebnissen von 0 bis 1500. Die zusammen ergeben höhe Wahrscheinlichkeit