Mit dem Satz der totalen Wahrscheinlichkeit kann man die Wahrscheinlichkeit für ein Ereignis
Als Beispiel sei hier die Parkinson-Krankheit genannt. Da mehr Männer als Frauen an Parkinson erkranken, sind hauptsächlich geschlechtsspezifische Zahlen veröffentlicht. Möchte man aber die Wahrscheinlichkeit der Erkrankung für eine zufällige Person unabhängig vom Geschlecht bestimmen, braucht man dafür den Satz der totalen Wahrscheinlichkeit. Mit Hilfe der Erkrankungsrate pro Geschlecht, dem Verhältnis von Frauen und Männern in der Gesamtbevölkerung, und der entsprechenden Formel erhält man dann die Gesamtwahrscheinlichkeit einer Parkinsonerkrankung.
In einem Venn-Diagramm kann man das Aufteilen einer totalen Wahrscheinlichkeit wie folgt illustrieren:
Es ist also
In unserem Beispiel der Parkinson-Krankheit hieße das: Die Wahrscheinlichkeit für eine beliebige Person, an Parkinson zu erkranken, setzt sich zusammen als die Summe der Wahrscheinlichkeit, ein Mann zu sein und an Parkinson zu erkranken, plus die Wahrscheinlichkeit, eine Frau zu sein und an Parkinson zu erkanken.
Meist sind nicht die gemeinsamen Wahrscheinlichkeiten
Wir erhalten also die verbreitetste Version der Formel für die totale Wahrscheinlichkeit:
Je nachdem, ob in einer Aufgabe die bedingten oder die gemeinsamen Wahrscheinlichkeiten gegeben sind, nimmt man die eine oder andere dieser beiden Formeln. In den allermeisten Fällen arbeitet man aber mit bedingten Wahrscheinlichkeiten.
Beispielaufgabe
Mit dieser Formel können wir nun für eine zufällige Person beliebigen Geschlechts die totale Wahrscheinlichkeit berechnen, an Parkinson zu erkranken. Wir benötigen dazu die folgenden Notationen:
Aus einer Onlinepublikation über die Prävalenz von Parkinson erhalten wir die folgenden Wahrscheinlichkeiten:
- Die Wahrscheinlichkeit für einen Mann, an Parkinson zu erkranken, liegt bei 0,309%. In unserer Formel bedeutet das:
- Die Wahrscheinlichkeit für eine Frau, an Parkinson zu erkranken, liegt bei 0,241%. Analog dazu:
- Es gibt minimal mehr Männer in der Gesamtbevölkerung, nämlich 51,1%. Also:
Mit diesen Werten können wir nun die Gesamtwahrscheinlichkeit für eine beliebige Person berechnen:
Wir enden also bei einer Wahrscheinlichkeit von 0,276% für eine Person beliebigen Geschlechts, an Parkinson zu erkranken. Wichtig ist hier, dass das nicht genau der Mittelwert zwischen
Mehr als zwei Gruppen in
Man kann die totale Wahrscheinlichkeit auch bestimmen, wenn es sich um mehr als zwei Gruppen handelt. Dann arbeitet man nicht mit den beiden Ereignissen
Für drei Untergruppen (und analog auch für beliebig viele Untergruppen) des Ereignisses

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!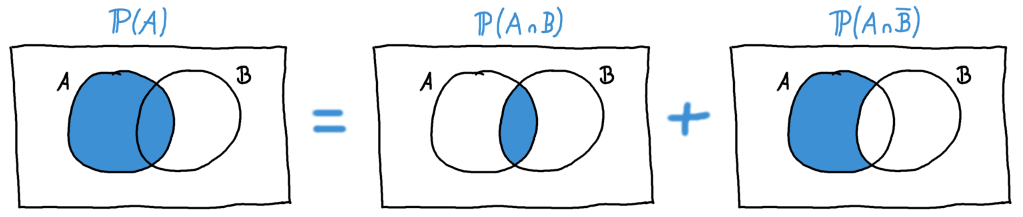
Ich habe nirgendwo bessere Erklaerungen finden koennen…
Danke sehr.
Danke, sehr hilfreich!
Endlich hab ich’s verstanden!!!
Danke Alex, klasse, was du hier bietest!