Das grosse Sigma (\(\Sigma\)) wird verwendet, um längere Summen in einer kurzen Schreibweise darzustellen. Meist wird das Zeichen verwendet, wenn man Kennziffern oder Teststatistiken für eine Stichprobe ausrechnet.
Wir werden hier als Beispiel das Lebensalter von fünf ARD-Zuschauern betrachten, und daraus einen Mittelwert berechnen.
| Person \(i\) | \(i=1\) | \(i=2\) | \(i=3\) | \(i=4\) | \(i=5\) |
|---|---|---|---|---|---|
| Alter \(x_i\) | 87 | 134 | 77 | 97 | 68 |
Wir messen hier das Merkmal \(x\), welches das Alter darstellen soll. Der Index \(i\) wird benutzt, um das Alter einer einzelnen Person darzustellen, zum Beispiel steht \(x_3\) für das Alter der dritten Person, \(x_3=77\).
Der Mittelwert \(\bar{x}\) lässt sich nun folgendermaßen berechnen:
\[ \bar{x} = \frac{1}{n} (x_1 + x_2 + x_3 + x_4 + x_5) = \frac{1}{n} \sum_{i=1}^n x_i \]
Das bedeutet nun, dass \(i\) eine Zählvariable ist, die von 1 bis \(n\) läuft (wir haben fünf Personen, also ist \(n=5\)). Es wird für jede Zählvariable \(i\) die Teilsumme \(x_i\) gebildet, und am Ende aufsummiert. In unserem Fall ist die Summe in ausgeschriebener Form:
\[ \begin{align*} \frac{1}{n} \sum_{i=1}^5 x_i & = \frac{1}{n} (x_1+x_2+x_3+x_4+x_5) \\ & = \frac{1}{5} (87+134+77+97+68) \\ & = 92.6 \end{align*} \]
Rechenregeln mit dem Summenzeichen
Man sollte vielleicht im Hinterkopf halten, dass Summen manchmal in einer abgekürzten Schreibweise aufgeschrieben werden. Wenn klar ist, über welche Zahlen die Zählvariable \(i\) laufen soll, findet man das Summenzeichen oft in Kurzform, zum Beispiel
\[\sum_{i=1}^n (x_i – \mu)^2 = \sum_i (x_i-\mu)^2.\]
Falls hinter dem Summenzeichen keine Klammer steht, die anzeigt, „wie weit“ die Summe geht, gilt im Allgemeinen diese Regel: Produkte und Potenzen gehören noch zum Summenzeichen dazu, aber ab dem ersten Plus bzw. Minus ist die Summe zu Ende:
\[\sum_{i=1}^3 i\cdot 2^2 + 5 = (1\cdot 2^2 + 2\cdot 2^2 + 3\cdot 2^2) + 5\]
Wenn man eine Summe, die durch das \(\Sigma\) dargestellt wird, in Gedanken in eine „normale“ Summe zerlegt, kann man die folgenden Rechenregeln leicht nachvollziehen, da sie direkt von ausgeschriebenen Summen abgeleitet werden können:
- \(\sum_i a \cdot x_i = a \cdot \sum_i x_i\)
- \(\sum_i (x_i + y_i) = \sum_i x_i + \sum_i y_i\)
- \(\sum_i (a x_i + b y_i) = \sum_i a x_i + \sum_i b y_i = a \sum_i x_i + b \sum_i y_i\)
Die erste Regel in dieser Liste ist das bekannte Ausklammern, und lässt sich nachvollziehen indem man die Summe ausschreibt:
\[\begin{align*}\sum_i a \cdot x_i & = a x_1 + a x_2 + a x_3 + \ldots \\ & = a \cdot (x_1 + x_2 + x_3 + \ldots) \\ & = a \cdot \sum_i x_i\end{align*}\]
Die anderen Regeln kann man auf dieselbe Weise ausschreiben und nachvollziehen.
Aufgabe
Stellen wir uns vor, es steht eine große Torte auf dem Tisch. Nacheinander laufen nun sehr, sehr viele Leute daran vorbei, und jeder nimmt sich die Hälfte von dem, das im Moment noch übrig ist. Die erste Person nimmt sich also die halbe Torte, die zweite Person die Hälfte vom Rest, d.h. eine Viertel Torte, die nächste Person nimmt sich ein Achtel, usw.
Die Torte wird nie komplett aufgegessen, aber doch immer kleiner. Den gesamten Anteil der Torte , der nach \(n\) Personen schon gegessen wurde, kann man durch eine Summe ausdrücken:
\[ \sum_{i=1}^n \frac{1}{2^i} \]
Um den Umgang mit dem Summenzeichen zu erlernen, bestimme, welcher Anteil der Torte nach \(n=3\) Personen aufgegessen wurde.

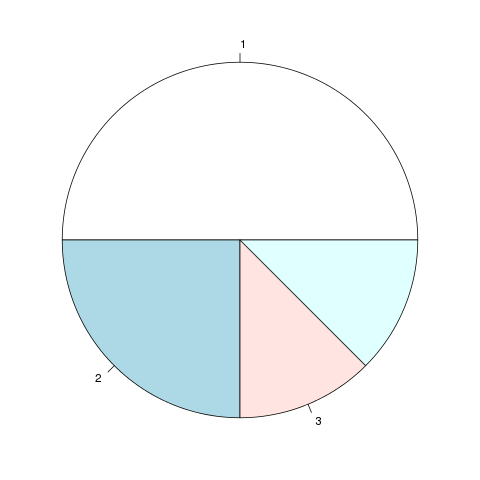
Hey, ich glaube, es wird durch ½ hoch i die Grösse des Reststückes dargestellt, denn nach der ersten Person ist ½ noch übrig, nach der zweiten ¼ und eben nicht noch ¾, denn wenn die Formel anzeigen würde, wie viel gegessen wurde, müssten nach der 2. Person dann laut Formel insgesamt erst ¼ gegessen sein, was nicht möglich ist, weil die erste person ja bereits ½ gegessen hat. Es ist bei der 2. Person ¼ übrig, daher zeigt die Formel an, wie viel noch übrig ist, respektive die Grösse des Reststücks.
Oops, habe gerade gemerkt, dass ich das Summenzeichen dabei vergessen habe. Dann ist alles richtig. Klar ist auch, dass das Gegenereignis zu „gegessen“ das von mir beschriebene Reststück ist, denn wie bei der Gegenwahrscheinlichkeit ergibt die Summe aus bereits gegessenem Kuchen und Reststück stets 1. Ich denke halt positiv, daher berechnete ich wohl automatisch das Reststück 😉
Hi,
du hast recht damit, dass die Größe des Reststücks durch \(\frac{1}{2}^i\) dargestellt wird.
Wieviel bereits gegessen wurde, wird durch die Summe dargestellt, also \(\sum_{i=1}^i \frac{1}{2}^i\). Bei zwei Personen ist \(i=2\), und die Summe ist dann 1/2 + 1/4, also 3/4.
Wenn ich dich richtig verstanden habe, war das das Mißverständnis. Es ist wichtig, ob man nur ein Glied der Summe betrachtet, oder die gesamte Summe.
VG,
Alex
Ups, jetzt war ich auch voreilig 🙂
Hallo,
es ist wohl beim ersten Beispiel ein Copy&Paste Fehler unterlaufen. Das Beispiel handelt von n = 5 (Personen und nicht Würfelseiten).
Des Weiteren ist bei der Aufgabe ein Unstimmigkeit. Unter dem Tortendiagramm wird nach der größe des Reststückes gefragt, oben jedoch nach dem bereits verspeisten Teil.
Viele Grüße
Dustin
Hi Dustin,
du hattest Recht. Ich hab die beiden Fehler korrigiert.
Vielen Dank für den Hinweis! 🙂
– Alex