Archiv der Kategorie: Allgemein

Stetige Gleichverteilung: Wartezeit auf den Bus

Idee

Die stetige Gleichverteilung ist quasi eine Verallgemeinerung der diskreten Gleichverteilung. Während bei der diskreten Gleichverteilung jede ganze Zahl zwischen \(a\) und \(b\) möglich ist (beim Würfelwurf ist z.B. \(a=1\) und \(b=6\)), so ist bei der stetigen Gleichverteilung nun jede reelle Zahl im Intervall von \(a\) bis \(b\) ein mögliches Ergebnis.

Ein einleuchtendes Beispiel für eine stetig gleichverteilte Zufallsvariable ist die Wartezeit auf einen Bus. Wenn ich weiß, dass der Bus alle 10 Minuten abfährt, aber den Fahrplan nicht im Kopf habe, sondern einfach an die Haltestelle laufe, dann folgt meine Wartezeit an der Haltestelle einer stetigen Gleichverteilung zwischen \(a=0\) und \(b=10\) Minuten. Hier ist nun jede reelle Zahl als Wartezeit möglich, z.B. auch 4.325 Minuten. Durch die Modellierung der Wartezeit als stetige Gleichverteilung kann ich nun zum Beispiel die durchschnittliche Wartezeit sowie ihre Varianz berechnen.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Parameter

Die stetige Gleichverteilung hat zwei Parameter, \(a\) und \(b\). Das sind die Intervallgrenzen. Es ist also \(a\) das kleinste mögliche Ergebnis der Zufallsvariablen, und \(b\) das größte mögliche. Eine Zufallsvariable \(X\), die stetig gleichverteilt ist, bezeichnet man durch

\[ X \sim \text{U}(a,b) \]

Das U kommt aus dem Englischen „uniform“, denn die Gleichverteilung heißt dort uniform distribution. Die Wartezeit in Minuten auf den nächsten Bus bezeichnet man etwa durch \(X \sim \text{U}(0,10)\).

Träger

Aus der Beschreibung der Parameter geht hervor, dass der Träger der stetigen Gleichverteilung genau das Intervall \([a,b]\) ist. Der Träger ist also \(\mathcal{T} = [a,b]\). An der Bushaltestelle sind so alle Wartezeiten zwischen 0 und 10 Minuten denkbar.

Dichte

Die Dichte setzt sich aus zwei Teilen zusammen: Außerhalb des Intervalls von \(a\) bis \(b\) ist sie überall 0, und innerhalb des Trägers \([a,b]\) ein gleichbleibender (konstanter) Wert, der abhängig von der Breite des Intervalls ist.

Der Wert der Dichte innerhalb des Intervalls ist \(f(x) = \frac{1}{b-a}\). Dadurch wird sichergestellt, dass die gesamte Fläche unter der Dichtefunktion 1 ergibt.

Außerhalb des Intervalls \([a,b]\) ist die Dichte überall null. Und damit gelangt man zur zweiteiligen Definition der Dichte:

\[ f(x) = \begin{cases} \frac{1}{b-a} &\mbox{falls } a \leq x \leq b \\ 0 & \mbox{sonst} \end{cases} \]

Der \(y\)-Wert der Dichtefunktion an der Stelle \(x\) ist also, falls \(x\) zwischen \(a\) und \(b\) liegt, gleich \(\frac{1}{b-a}\), und für alle anderen \(x\) gleich null.

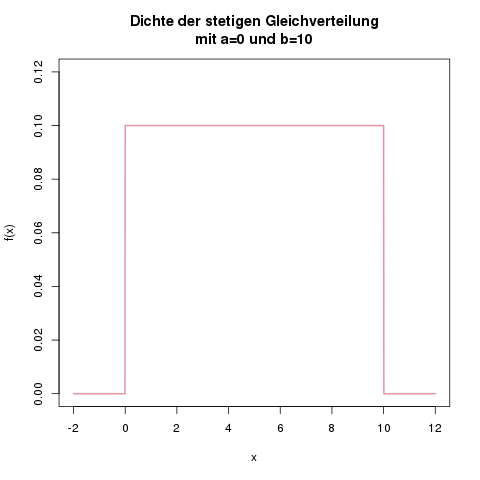
Die Dichte der stetigen Gleichverteilung mit \(a=0\) und \(b=10\). Sie ist überall null, und im Bereich von 0 bis 10 gleich \(\frac{1}{10}\).

Verteilungsfunktion

Die Verteilungsfunktion ist nun dreiteilig definiert: Links von der unteren Grenze \(a\) ist sie überall null, da die Wahrscheinlichkeit, dass \(X\) einen Wert kleiner als \(a\) annimmt, null ist: \(\mathbb{P}(X \leq a) = 0\). Rechts von der oberen Grenze \(b\) ist sie konstant 1, da auf jeden Fall ein Wert kleiner oder gleich \(b\) herauskommt: \(\mathbb{P}(X \leq b) = 1\).

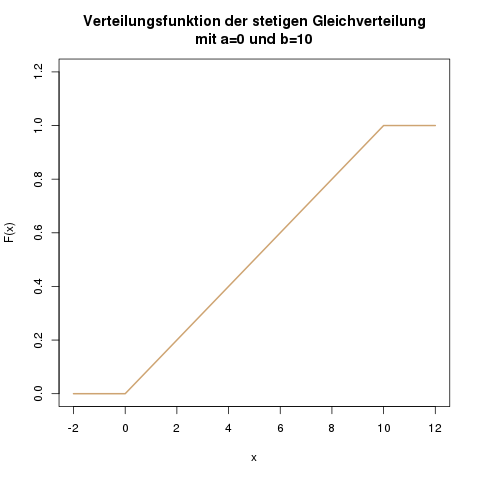
Die Verteilungsfunktion aus dem Beispiel der Wartezeit auf den Bus sieht wie folgt aus:

Die Verteilungsfunktion der stetigen Gleichverteilung, hier mit \(a=0\) und \(b=10\).

Innerhalb des Intervalls von \(a\) bis \(b\) ist die Verteilungsfunktion eine gerade Linie von 0 bis 1. In einer Formel drückt man diese Linie durch \(\frac{x-a}{b-a}\) aus. Der Nenner ist hier an jeder Stelle von \(x\) eine Konstante. Der Zähler ist an der Stelle \(x=a\) genau null, und wird dann in Richtung \(b\) immer größer.

Das führt zu einer dreiteiligen Definition der Verteilungsfunktion:

\[ F(x) = \begin{cases} 0 &\mbox{falls } x < a \\ \frac{x-a}{b-a} &\mbox{falls } a \leq x \leq b \\ 1 & \mbox{falls } x>b \end{cases} \]

Bei der Wartezeit auf den Bus, mit \(a=0\) und \(b=10\), können wir also zum Beispiel die folgenden Werte ablesen:

Die Wahrscheinlichkeit, dass wir weniger als -2 Minuten warten, ist null: \(\mathbb{P}(X \leq -2) = F(-2) = 0\). Wir warten also auf jeden Fall eine positive Zeit (das macht auch Sinn).
Die Wahrscheinlichkeit, dass wir maximal 3 Minuten warten, berechen wir durch \(\mathbb{P}(X \leq 3) = F(3) = \frac{3 – 0}{10 – 0} = 0.3\). Wir warten also mit einer 30-prozentigen Wahrscheinlichkeit weniger als 3 Minuten.
Umgekehrt warten wir mit einer 70-prozentigen Wahrscheinlichkeit mehr als 3 Minuten, denn \(\mathbb{P}(X > 3) = 1 – \mathbb{P}(X \leq 3) = 1 – 0.3 = 0.7\).
Wie im allgemeinen Artikel zu stetigen Zufallsvariablen beschrieben, können wir auch die Wahrscheinlichkeit berechnen, zwischen 3 und 5 Minuten auf den Bus zu warten. Das ist nämlich \(\mathbb{P}(3 < x \leq 5) =\mathbb{P}(x \leq 5) -\mathbb{P}(x \leq 3) = F(5)-F(3) = 0.5 – 0.3 = 0.2\).
Die Wahrscheinlichkeit, dass wir höchstens 30 Minuten warten, ist 1, denn der Bus kommt alle 10 Minuten (wir modellieren hier keine außergewöhnlichen Verspätungen): \(\mathbb{P}(X \leq 30) = F(30) = 1\).

Erwartungswert

Der Erwartungswert bei der Gleichverteilung ist genau die Mitte zwischen \(a\) und \(b\):

\[ \mathbb{E}(X) = \frac{a+b}{2} \]

Auf den Bus, der alle zehn Minuten kommt, warten wir also durchschnittlich \(\frac{0+10}{2} = 5\) Minuten.

Varianz

Die Varianz berechnet sich zu

\[ \mathbb{V}(X) = \frac{1}{12}(b-a)^2 \]

Das Produktzeichen und Rechenregeln

3 Antworten

Das Pendant zum Summenzeichen \(\Sigma\) für die Multiplikation ist das Produktzeichen \(\Pi\), ein großes Pi. Mit diesem Zeichen kann man Multiplikationen über viele Variablen zusammenfassen. Diese Notation sieht für Nicht-Mathematiker auf den ersten Blick immer etwas furchteinflößend aus, aber wenn man versteht, dass es einfach nur eine Abkürzung für eine längere Formel ist, kommt man gut mit dieser Schreibweise zurecht.

Statt ausführlich \(1 \cdot 2 \cdot 3 \cdot 4 \cdot 5\) zu schreiben, kann man nämlich einfach eine Zählvariable \(i\) von 1 bis 5 laufen lassen, und diese Zählvariablen multiplizieren:

\[ \prod_{i=1}^5 i = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \]

Diese Notation ist übrigens äquivalent zur Fakultät von 5. Es ist also \(x! = \prod_{i=1}^x i\).

Wenn man nicht über Ganzzahlen, sondern z.B. gemessene Daten \(x_1,x_2,x_3,x_4,x_5\) multiplizieren möchte, kann man auch über den Index der Variablen \(x\) laufen:

\[ \prod_{i=1}^5 x_i =x_1 \cdot x_2 \cdot x_3 \cdot x_4 \cdot x_5 \]

Die Variable hinter dem \(\Pi\) ist jetzt nicht mehr nur ein \(i\), sondern ein Datenpunkt \(x_i\). Man muss sich merken, dass der Index, der unter dem \(\Pi\) steht, eine Zählvariable ist, die in diesem Fall von 1 bis 5 läuft. Wenn man genau diesen Index \(i\) multiplizieren will, dann steht eben nur ein \(i\) nach dem \(\Pi\), aber wenn man Datenpunkte \(x_i\) muliplizieren will, dann ersetzt man das \(i\) durch ein \(x_i\).

Da sich hinter dem Produktzeichen eine ganz normale Multiplikation verbirgt, gelten dafür dieselben Rechenregeln wie für die normale Multiplikation:

Nach dem Distributivgesetz kann man bei der Multiplikation die Reihenfolge der Faktoren vertauschen. Es gilt also z.B. \(x_1 \cdot y_1 \cdot x_2 \cdot y_2 =x_1 \cdot x_2 \cdot y_1 \cdot y_2\). Genauso gilt das Distributivgesetz auch mit dem Produktzeichen:
\[ \prod_{i=1}^n (x_iy_i) = \prod_{i=1}^n x_i \cdot \prod_{i=1}^n y_i \] Wenn man diese Formel anhand eines kurzen Beispielfalls ausschreibt, sieht man, dass hier tatsächlich nur die Reihenfolge vertauscht wurde.
Wenn man eine konstante Zahl \(n\)-mal mit sich selbst multipliziert, erhält man ihre \(n\)-te Potenz:
\[ \prod_{i=1}^n c = c^n \] Die Zahl \(c\) ist hier nicht vom Index \(i\) abhängig. Daher wird einfach nur \(c\) multipliziert. Es gilt also \(\prod_i c = c \cdot c \cdot \ldots \cdot c = c^n\).
Man kann ebenso eine Konstante aus einem Produkt herausziehen, wenn noch andere Faktoren mit dabei stehen. Es gilt also zum Beispiel
\[ \prod_{i=1}^3 c x_i = c x_1 \cdot c x_2 \cdot c x_3 = c^3 \prod_{i=1}^3 x_i \] Allgemein ausgedrückt lautet diese Formel
\[ \prod_{i=1}^n c x_i = c^n \prod_{i=1}^n x_i \]

Exponentialfunktion und Logarithmusfunktion

Schreibe eine Antwort

Potenzen

Bevor wir Polynome und Exponentialfunktionen besprechen, frischen wir die Grundlagen über Potenzen nocheinmal auf.

Potenzen sind, einfach ausgedrückt, eine Kurzschreibweise für wiederholte Multiplikation. Genauso wie man statt \(4+4+4+4+4\) einfach kurz \(5\cdot 4\) schreiben kann, so kann man \(3\cdot 3\cdot 3\cdot 3\cdot 3\) durch \(3^5\) abkürzen. Hier bezeichnet man die \(3\) als Basis, und die \(5\) als Exponent.
Der Sonderfall \(x^0=1\) ist so definiert, da wir quasi „null“ Multiplikationen vornehmen, also nur das bei der Multiplikation neutrale Element 1 übrigbleibt.

Negative Exponenten verwendet man für wiederholte Division. Es gilt also z.B.

\[ 2^{-4} = 1 \div 2 \div 2 \div 2 \div 2 = \frac{1}{2^4} \]

Brüche als Exponenten bezeichnen Wurzeln. Zum Beispiel bedeutet \(5^\frac{1}{2}\) dasselbe wie \(\sqrt{5}\), und \(2^\frac{1}{3}\) ist gleichbedeutend mit \(\sqrt[3]{2}\).
Falls im Zähler des Bruches eine andere Zahl als 1 steht, ist das die Potenz der Basis unter dem Bruch:

\[ 2^\frac{3}{4} = \sqrt[4]{2^3} \]

Reelle Exponenten, also zum Beispiel \(3^{3.1415926\ldots}\), sind nicht mehr ganz so intuitiv zu erklären. Man kann sich den Exponenten am besten als Interpolation zweier ihm nahe liegender Brüche vorstellen.

Rechenregeln für Potenzen gibt es einige. Die wichtigsten sind in der folgenden Übersicht zusammengefasst – links die allgemeine Regel, rechts ein veranschaulichendes Beispiel:

\(x^a \cdot x^b = x^{a+b}\)	\(x^3 \cdot x^2 = x \cdot x \cdot x \cdot x \cdot x = x^5 = x^{2+3}\)
\(\frac{x^a}{x^b} = x^{a-b}\)	\(\frac{x^4}{x^2} = \frac{x \cdot x \cdot x \cdot x}{x \cdot x} = x^2 = x^{4-2}\)
\((x^r)^s = x^{r\cdot s}\)	\((x^2)^2 = x^2 \cdot x^2 = x \cdot x \cdot x \cdot x = x^{2\cdot 2}\)
\(\left(\frac{x}{y}\right)^r = \frac{x^r}{y^r}\)	\(\left(\frac{x}{y}\right)^3 = \frac{x}{y}\frac{x}{y}\frac{x}{y} = \frac{x^3}{y^3}\)
\((x\cdot y)^r = x^r \cdot y^r\)	\((x\cdot y)^2 = (x\cdot y) \cdot (x\cdot y) = x^2 y^2\)

Exponentialfunktion

Die Exponentialfunktion ist eine in der Statistik sehr häufig verwendete Funktion, denn sie kommt in den meisten stetigen und diskreten Dichten vor. Was es damit auf sich hat, werden wir hier besprechen.

Die meisten sind wohl vertraut mit Polynomialfunktionen wie \(f(x) = x^3\). Hier ist die Basis (hier \(x\)) die Variable, und der Exponent (hier \(3\)) eine konstante Zahl. Die dazugehörigen Kurven sehen beispielsweise wie folgt aus:

Beispiele für Polynomfunktionen: Die Kurven für \(x^a\) mit \(a=1,2,3,4,5\).

Von der Polynomfunktion zur Exponentialfunktion gelangt man nun, wenn man nicht die Basis variiert, sondern den Exponenten. Wir nehmen also nicht \(f(x)=x^2\), sondern stattdessen \(f(x)=2^x\). Exponentialfunktionen sehen wie folgt aus:

Die Exponentialfunktionen für die Basis 1, 2, \(e\), und 3. Die Funktion \(f(x)=1^x\) ist konstant 1, da z.B. \(1^3=1\) ist.

Hier fallen die folgenden Dinge auf:

Alle Exponentialfunktionen haben an der Stelle 0 den Wert 1, da \(a^0=1\), egal für welches \(a\).
Im negativen Bereich nehmen die Funktionen Werte zwischen 0 und 1 an, da die negativen Exponenten in diesem Bereich wie oben besprochen zu einem Bruch führen, der kleiner als 1 ist.
Je größer die Basis ist, desto steiler steigt die Exponentialfunktion an.

Die Funktionen haben den Definitionsbereich \(\mathbb{R}\), denn jede reelle Zahl kann im Exponenten stehen. Weil die Funktion aber nur Werte im positiven Bereich liefert, ist ihr Wertebereich \(\mathbb{R}^+\), die reellen Zahlen größer als Null.

Eine besondere Basis ist die eulersche Zahl \(e\). Sie ist ungefähr \(e \approx 2.71828\) und wird in Dichtefunktionen häufig als Basis verwendet. Dargestellt wird sie häufig in Termen wie \(e^{-\frac{1}{2}x^2}\), oder in der alternativen Schreibweise \(\exp (-\frac{1}{2}x^2)\).

Rechenregeln für die Exponentialfunktion lassen sich anhand der Rechenregeln für Potenzen ableiten. Da, wie oben besprochen, zum Beispiel \(x^a \cdot x^b = x^{a+b}\) gilt, ist genauso mit der Basis \(e\) die folgende Gleichung gültig: \(\exp (a) \cdot \exp (b) = \exp (a+b)\).

Mit dem Summenzeichen kann man diese Formel noch auf längere Summen erweitern, und es gilt:

\[ \prod_{i=1}^n \exp (x_i) = \exp (\sum_{i=1}^n x_i) \]

Logarithmusfunktion

Der Logarithmus ist die Umkehrfunktion zur Exponentialfunktion. Mit einer Umkehrfunktion kann man eine Transformation quasi rückgängig machen. Es ist zum Beispiel die Wurzelfunktion die Umkehrfunktion zur Quadratfunktion, denn mit ihr kann man eine Quadrierung wieder rückgängig machen:

\[ \begin{align*} 3^2 &= 9 \\ \sqrt{9} &= 3 \end{align*} \]

Genauso kann man mit dem Logarithmus einer Zahl, der als \(\log (x)\) dargestellt wird, eine Exponentialfunktion wieder rückgängig machen. Es ist also zum Beispiel

\[ \begin{align*} \exp (3) &\approx 20.086 \\ \log (20.086) &\approx 3 \end{align*} \]

In diesem Beispiel interpretiert man den Logarithmus so: „\(e\) hoch wieviel ist 20.086?“. Der Logarithmus gibt die Antwort auf diese Frage.

Auf der linken Grafik sieht man die Exponentialfunktion \(f(x) = \exp (x)\). Hier kann man ablesen, dass \(\exp (3)\) in etwa 20 ist. Auf der rechten Grafik ist die Logarithmusfunktion, \(f(x) = \log (x)\), dargestellt. Hier kann man die erhaltenen 20 wieder umkehren in \(\log (20) \approx 3\).

Genauso wie es bei Exponentialfunktionen eine Basis gibt (wie z.B. die Basis \(10\) bei der Funktion \(f(x) = 10^x\), so bezieht sich auch ein Logarithmus immer auf eine Basis. Der natürliche Logarithmus, den wir bisher betrachtet haben, bezieht sich auf die Basis \(e\). Die verbreitetsten anderen Logarithmen ist der Zweierlogarithmus mit der Basis 2, und der Zehnerlogarithmus mit der Basis 10. Am eindeutigsten notiert man den Logarithmus, indem man die Basis unter das Log-Symbol schreibt, also z.B. \(\log_{10}\) oder \(\log_2\). Wenn keine Zahl als Basis hinzugefügt wurde, meint ein „nacktes“ \(\log\)-Symbol zumindest im statistischen Bereich immer den natürlichen Logarithmus, zur Basis \(e\). In manchen angewandten Gebieten kann damit allerdings auch der Zehnerlogarithmus gemeint sein, dort wird dann \(\ln\) für den natürlichen Logarithmus verwendet. Wegen dieser Möglichkeit der Verwechslung ist es empfohlen, die Basis immer explizit dazuzuschreiben.

Der Zehnerlogarithmus ist besonders leicht zu interpretieren, da die Zehnerpotenzen (10, 100, 1000, usw.) eine ganze Zahl ergeben. Er findet oft in Grafiken Anwendung, wo er zur Transformation von Daten verwendet wird, die man in ihrer untransformierten Darstellung schlecht erkennen kann. Das sind meistens Daten, die eine schiefe Verteilung haben – als Beispiele kann man sich das Nettoeinkommen in einer großen Firma, oder die Einwohnerzahl aller deutschen Städte vorstellen.

Die Einwohnerzahlen aller deutschen Großstädte (>100.000 Einwohner). Oben sieht man die untransformierten Daten, und eine sehr schiefe Verteilung, in der sich fast alle Punkte zwischen 100.000 und 500.000 aufhalten. Die vier Städte rechts der 1Mio-Marke sind Berlin, Hamburg, München und Köln. In der unteren Grafik sind die Daten nur mit dem Zehnerlogarithmus transformiert. Man hat hier eine bessere Übersicht über die Streuung der Daten in den niedrigen Bereichen. Da \(\log_{10} (1.000.000) = 6\) ist, sind die vier Millionenstädte in der unteren Grafik die, die rechts der \(6.0\) liegen.

Da das Ergebnis einer Exponentialfunktion nur positiv sein kann, kann man umgekehrt den Logarithmus auch nur von einer positiven Zahl nehmen. Ein Wert wie z.B. \(\log (-3)\) ist nicht definiert. Der Definitionsbereich für die Logarithmusfunktion ist also \(\mathbb{R}^+\), die gesamten positiven reellen Zahlen. Der Wertebereich hingegen sind die gesamten reellen Zahlen \(\mathbb{R}\).

Rechenregeln für den Logarithmus gibt es natürlich auch. Die wichtigsten sind in der folgenden Tabelle zusammengefasst, wobei links die allgemeine Regel, und rechts eine Anwendung der Regel steht:

Regel	Beispiel
\(\log \left( \exp (x) \right) = x\)	\(\log_{10}(10^8) = 8\)
\(\exp \left( \log (x) \right) = x\)	\(10^{\log_{10}(8)} = 8\)
\(\log ( x \cdot y ) = \log (x) + \log (y)\)	\(\log (\prod_{i=1}^n x_i) = \sum_{i=1}^n \log (x_i)\)
\(\log ( \frac{x}{y} ) = \log (x) – \log (y)\)	\(\log (\frac{1}{3}) = \log (1) – \log (3)\)
\(\log (x^r) = r \cdot \log (x)\)	\(\log (\sqrt{x}) = \log (x^{\frac{1}{2}}) = \frac{1}{2} \log (x)\)

Poissonverteilung: Anzahl an Toren pro Fußballspiel

Schreibe eine Antwort

Idee

Die Poissonverteilung ist eine diskrete Verteilung, mit der man die Anzahl von Ereignissen in einem gegebenen Zeitintervall modellieren kann. Ein schönes Beispiel ist die Anzahl von Toren, die Verein \(A\) innerhalb eines Fußballspiels schießt. Andere Anwendungen sind etwa die Anzahl an Bankkunden, die innerhalb eines Tages am Schalter ankommen, oder die Anzahl an Schadensfällen, die in einem Monat bei einer Versicherung eingehen.

Man zählt in jedem dieser Fälle die Anzahl der Ereignisse, die in einem fest vorgegebenen Zeitintervall eintreten, und möchte die Wahrscheinlichkeiten modellieren, mit der \(x\) Ereignisse in diesem Zeitraum auftreten.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Parameter

Die Poissonverteilung hat nur einen Parameter, nämlich \(\lambda\). Er bezeichnet die durchschnittlich zu erwartende Anzahl an Ereignissen (also den Erwartungswert). Eine poissonverteilte Zufallsvariable \(X\) bezeichnet man dann durch

\[ X \sim \text{Po}(\lambda) \]

Man könnte nun zum Beispiel für 100 Fußballspiele vom Verein \(A\) die Anzahl seiner geschossenen Tore notieren, und deren Mittelwert ausrechnen. Wenn der Mittelwert 1.2 Tore sind, dann wäre in diesem Fall \(X \sim \text{Po}(1.2)\).

Träger

Bei einem Poisson-Experiment können zwischen null und unendlich viele Ereignisse eintreten. Im Beispiel mit dem Fußballspiel sind theoretisch unbegrenzt viele Tore möglich. Der Träger einer poissonverteilten Zufallsvariable ist also

\[ \mathcal{T}(X) = \{ 0, 1, 2, \ldots \} \]

Dichte

Die Wahrscheinlichkeit, dass bei einer poissonverteilten Zufallsvariable mit dem Parameter \(\lambda\) genau \(x\) Ereignisse auftreten, berechnet man über die Dichte zu

\[ f(x) = \frac{\lambda^x}{x!} \exp (-\lambda) \]

Dabei bezeichnet \(x! \) die Fakultät von \(x\). Falls man die Wahrscheinlichkeit für 0 Ereignisse berechnen möchte, tritt hier \(0! \), die Fakultät von null, auf. Das ist definitionsgemäß gleich eins.

Im Beispiel mit dem Fußballverein berechnet man etwa die Wahrscheinlichkeit, dass Verein \(A\) genau zwei Tore schießt, zu

\[ f(2) = \frac{1.2^2}{2!} \exp (-1.2) = 0.217 \]

Die Dichte der Poissonverteilung für die Anzahl der von Team \(A\) geschossenen Tore in einem Spiel, mit \(\lambda=1.2\). Die \(x\)-Achse ist hier bei 7 abgeschnitten: Höhere Werte als \(x=7\) sind theoretisch möglich, aber sehr unwahrscheinlich. Man sieht hier auch, dass mit der höchsten Wahrscheinlichkeit ein Tor geschossen wird.

Zwischenaufgabe

Angenommen, die Anzahl der Tore von Team \(A\) ist tatsächlich poissonverteilt mit \(\lambda=1.2\). Ein Freund wettet um 10€ mit dir, dass das Team im folgenden Spiel genau ein Tor schießt, da das die Anzahl mit der höchsten Wahrscheinlichkeit ist. Solltest du diese Wette annehmen?

Lösung (klick)

Deine Gewinnwahrscheinlichkeit ist die Summe aller einzelnen Wahrscheinlichkeiten \(f(x)\) für \(x\) Tore, außer für \(x=1\). Man kann natürlich nicht \(f(0)+f(2)+f(3)+f(4)+\ldots\) berechnen, sondern geht hier wieder mit der Gegenwahrscheinlichkeit vor. Wir berechen also nicht \(\mathbb{P}(\text{alles ausser ein Tor})\), sondern stattdessen äquivalent \(1-\mathbb{P}(\text{ein Tor})\):

\[ 1 – f(1) = 1 – \frac{1.2^1}{1!} \exp (-1.2) = 1-0.3614 = 0.639 \]

Da wir mit einer Wahrscheinlichkeit von etwa 63,9% gewinnen, sollten wir diese Wette also annehmen. Obwohl das Ereignis mit der höchsten einzelnen Wahrscheinlichkeit ein Tor ist, so ist es doch wahrscheinlicher, dass irgendein anderes Ergebnis eintritt.

Verteilungsfunktion

Für die Verteilungsfunktion gibt es keine bequeme Formel. Man muss für \(F(x) = \mathbb{P}(X \leq x)\) die einzelnen Werte der Dichtefunktion von 0 bis \(x\) aufsummieren:

\[ F(x) = f(0) + f(1) + \ldots + f(x) = \sum_{k=0}^x f(k) \]

Die Wahrscheinlichkeit dass unser Verein höchstens zwei Tore schießt, berechnet man also durch

\[ \begin{align*} F(2) &= f(0) + f(1) + f(2) \\&= \frac{1.2^0}{0!} \exp(-1.2) + \frac{1.2^1}{1!} \exp(-1.2) + \frac{1.2^2}{2!} \exp(-1.2) \\&= 0.301 + 0.361 + 0.217 \\&= 0.879 \end{align*} \]

Die Verteilungsfunktion für die Anzahl der Tore von Verein \(A\). Man sieht, dass die Wahrscheinlichkeit \(F(4)\) für maximal vier Tore schon sehr nahe an der 1 liegt, dass es also andersherum sehr unwahrscheinlich ist, dass Team \(A\) in einem Spiel mehr als vier Tore schießt.

Erwartungswert und Varianz

Der Parameter \(\lambda\) einer poissonverteilten Zufallsvariable ist zugleich Erwartungswert und Varianz dieser Verteilung:

\[ \begin{align*} \mathbb{E}(X)&=\lambda \\ \mathbb{V}(X)&=\lambda \end{align*} \]

Eigenschaften

Die folgenden Regeln sind hilfreich für kompliziertere Aufgaben mit der Poissonverteilung.

Wenn die Anzahl der Tore von Verein \(A\) innerhalb eines 90-minütigen Spiels poissonverteilt mit \(\lambda = 1.2\) ist, dann ist die Anzahl der Tore innerhalb der ersten Halbzeit auch poissonverteilt, aber mit \(\lambda = 0.6\).
Allgemein gesagt: Wenn der betrachtete Zeitraum mit einem Faktor \(n\) multipliziert wird, ist die Anzahl der Ereignisse in diesem Zeitraum poissonverteilt mit dem Parameter \(\lambda \cdot n\).
Die Wahrscheinlichkeit, dass mindestens ein Ereignis eintritt, ist das Gegenteil der Wahrscheinlichkeit dass gar kein Ereignis auftritt, und somit \(1-f(0)\).
Verein \(A\) schießt also mit einer Wahrscheinlichkeit von \(1-\frac{1.2^0}{0!} \exp (-1.2) = 0.699\) mindestens ein Tor.
Wenn die Anzahl der Tore von Verein \(A\) poissonverteilt mit \(\lambda_A=1.2\), und die Anzahl der Tore seines Gegners, Verein \(B\), poissonverteilt mit \(\lambda_B=0.6\) ist, dann ist die Gesamtzahl der gefallenen Tore im Spiel von \(A\) gegen \(B\) wieder poissonverteilt mit \(\lambda = \lambda_A + \lambda_B = 1.8\).
Allgemein gilt: Die Summe zweier unabhängiger poissonverteilten Zufallsvariablen \(A\) und \(B\) mit den Parametern \(\lambda_A\) und \(\lambda_B\) ist poissonverteilt mit dem Parameter \(\lambda = \lambda_A+\lambda_B\).

Geometrische Verteilung: Der betrunkene Pförtner

Schreibe eine Antwort

Idee

Bei der geometrischen Verteilung liegt folgender Gedanke zugrunde: Wir haben ein Bernoulli-Experiment mit einer Erfolgswahrscheinlichkeit von \(p\). Nun fragen wir uns, wie oft wir dieses Experiment ausführen müssen, bis der erste Erfolg eintritt.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Das meiner Meinung nach schönste Beispiel zur Veranschaulichung ist das vom betrunkenen Pförtner: Er hat einen Schlüsselbund mit 8 Schlüsseln, und einer davon öffnet das Tor, vor dem er steht. Da er aber betrunken ist, fällt ihm nach jedem Fehlversuch der Schlüsselbund herunter, und er weiß nicht mehr, welchen Schlüssel er schon probiert hat.

Jeder einzelne Versuch ist also ein neues Bernoulli-Experiment mit der Erfolgswahrscheinlichkeit \(p=\frac{1}{8}\). Da er 8 Schlüssel hat, ist ein zufällig gewählter Schlüssel mit einer Wahrscheinlichkeit von \(\frac{1}{8}\) der richtige.

Mit der geometrischen Verteilung können wir dieses Experiment nun beschreiben, und die Wahrscheinlichkeiten dafür bestimmen, dass er zum Beispiel genau einen Versuch, genau vier Versuche, oder höchstens fünf Versuche benötigt.

Parameter

Die geometrische Verteilung hat nur einen Parameter, nämlich \(p\), die Erfolgswahrscheinlichkeit bei einem einzelnen Versuch. Im Beispiel des betrunkenen Pförtners ist \(p=\frac{1}{8}\). Benennen wir die Zufallsvariable für das Experiment mit \(X\), wird die geometrische Verteilung dargestellt durch

\[ X \sim \text{G}(p), \]

in unserem Beispiel

\[ X \sim \text{G}(\frac{1}{8}). \]

Träger

Es gibt theoretisch keine Obergrenze für die Anzahl der Versuche, die der Pförtner benötigt. Jeder neue Versuch gelingt nur mit einer Wahrscheinlichkeit von \(\frac{1}{p}\), daher kann \(X\) jede natürliche Zahl von 0 bis unendlich annehmen:

\[ \mathcal{T} = \{ 0, 1, 2, \ldots \} \]

Dichte

Die Dichte der geometrischen Verteilung lautet

\[ f(x) = (1-p)^{x-1} p \]

Diese Dichte kann man sich leicht veranschaulichen: Um die Wahrscheinlichkeit zu bestimmen, dass der Pförtner beim dritten Versuch den richtigen Schlüssel erwischt, also \(\mathbb{P}(X=3) = f(3)\), muss er nacheinander zwei Fehlversuche (mit Wahrscheinlichkeit \(1-p\) und einen Treffer (mit Wahrscheinlichkeit \(p\)) machen. Die gesamte Wahrscheinlichkeit ist also das Produkt der drei Bernoulli-Experimente, also \((1-p)\cdot (1-p) \cdot p\). Das kann man zu \((1-p)^2 \cdot p\) zusammenfassen. Setzt man nun allgemein ein \(x\) statt der 2 ein, erhält man die Dichte der geometrischen Verteilung, nämlich das Produkt von \(x-1\) Mißerfolgen und einem Erfolg.

Die Dichte der geometrischen Verteilung für das Beispiel des betrunkenen Pförtners. Die \(x\)-Achse ist abgeschnitten, da die Dichte nach rechts ins Unendliche weitergeht. Die Wahrscheinlichkeiten für mehr als ca. 30 Versuche werden verschwindend gering, aber sind theoretisch immer noch im Bereich des Möglichen. Man sieht auch, dass \(f(1)\), die Wahrscheinlichkeit, dass gleich beim ersten Versuch der Treffer erfolgt, genau \(p\) ist.

Verteilungsfunktion

Die Verteilungsfunktion lässt sich mit Hilfe einer Rechenregel für Wahrscheinlichkeiten herleiten. Wir suchen nämlich gemäß der Definition der Verteilungsfunktion den Wert \(\mathbb{P}(X \leq x)\), also die Wahrscheinlichkeit, dass der Pförtner maximal \(x\) Versuche benötigt, um das Tor zu öffnen. Dieser Wert ist nur über eine Summe der Dichten von \(f(0)\) bis \(f(x)\) zu erhalten. Aber die Gegenwahrscheinlichkeit ist einfach:

Die Wahrscheinlichkeit \(\mathbb{P}(X > x)\), dass der Pförtner mehr als \(x\) Versuche benötigt, ist leicht zu berechnen. Es ist nämlich das Produkt von \(x\) Fehlversuchen, also \((1-p)^x\). Und das ist genau das Gegenereignis vom Ereignis „maximal \(x\) Versuche“.

Mit der folgenden Regel erhalten wir dann die Verteilungsfunktion:

\[ \mathbb{P}(\bar{A}) = 1-\mathbb{P}(A) \]

Die Verteilungsfunktion der geometrischen Verteilung ist also

\[ F(x) = \mathbb{P}(X \leq x) = 1-\mathbb{P}(X > x) = 1-(1-p)^x \]

Die Verteilungsfunktion der geometrischen Verteilung. Ihr Wert nähert sich im Unendlichen der 1 an, erreicht ihn aber nie exakt.

Erwartungswert

Der Erwartungswert der geometrischen Verteilung ist

\[ \mathbb{E}(X) = \frac{1}{p} \]

Bei 8 Schlüsseln, also \(p=\frac{1}{8}\), braucht der Pförtner also im Durchschnitt 8 Versuche, um das Tor zu öffnen.

Varianz

Die Varianz der geometrischen Verteilung berechnet man durch

\[ \mathbb{V}(X) = \frac{1}{p^2} – \frac{1}{p} \]

Alternative Darstellung

In manchen Büchern bzw. Skripten begegnet man auch einer alternativen Darstellung der geometrischen Verteilung. Hier ist mit \(X\) nicht wie hier die Anzahl der Versuche bis (inklusive!) zum ersten Treffer gemeint, sondern die Anzahl der Fehlversuche vor dem ersten Treffer. Wenn ich also modellieren will, dass der betrunkene Pförtner drei Fehlversuche macht, bis er im vierten Versuch das Tor öffnet, so berechne ich in der hier besprochenen Darstellung \(f(4)\), aber in dieser alternativen Darstellung wäre es stattdessen \(f(3)\). Die Formeln für Dichte, Verteilungsfunktion, und Erwartungswert verändern sich natürlich entsprechend, so dass dieselben Wahrscheinlichkeiten herauskommen.

Hypergeometrische Verteilung

11 Antworten

Idee

Während die Binomialverteilung für Experimente mit gleichbleibender Wahrscheinlichkeit für „Erfolg“ verwendet wird, wendet man die hypergeometrische Verteilung dann an, wenn sich die Grundgesamtheit im Laufe des Experiments verändert. Anders ausgedrückt: Mit der Binomialverteilung beschreibt man Experimente mit Zurücklegen, und mit der hypergeometrischen Verteilung Experimente ohne Zurücklegen.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Habe ich also einen Beutel mit 10 roten und 5 weißen Kugeln, und nehme viermal hintereinander eine Kugel aus dem Beutel, die ich danach wieder zurücklege, so dass wieder insgesamt 15 Kugeln im Beutel sind, dann kann ich mit der Binomialverteilung die Verteilung der Anzahl der gezogenen weißen Kugeln beschreiben. Das wäre nämlich eine Binomialverteilung mit \(n=4\) und \(p=\frac{5}{15} = \frac{1}{3}\). Hier fällt auf, dass die genaue Anzahl an Kugeln egal ist, und nur ihr Verhältnis zueinander interessiert. Das Experiment wäre also genau dasselbe, wenn nicht 10 rote und 5 weiße, sondern 100 rote und 50 weiße Kugeln in dem Beutel steckten.

Möchte man stattdessen die Kugeln nicht zurücklegen, verwendet man die hypergeometrische Verteilung. Das Experiment, das man mit ihr modellieren kann, sieht also zum Beispiel wie folgt aus: Man hat einen Beutel mit 15 Kugeln, wovon 5 Kugeln weiß sind. Man nimmt nun nacheinander vier Kugeln aus dem Beutel, ohne sie danach zurückzulegen. Nun kann ich mit Hilfe der hypergeometrischen Verteilung ausrechnen, mit welcher Wahrscheinlichkeit ich keine, eine, zwei, drei, oder vier weiße Kugeln in meiner Stichprobe erhalte.

Parameter

Für die hypergeometrische Verteilung ist es nun im Gegensatz zur Binomialverteilung wichtig, wieviele Kugeln jeder Sorte im Beutel liegen. Daher hat diese Verteilung drei Parameter:

\(N\), die Anzahl der Elemente insgesamt. Im oberen Beispiel haben wir \(N=15\) Kugeln.
\(M\), die Anzahl der Elemente, die die gewünschte Eigenschaft besitzen („Treffer“). Hier ist \(M=5\), die Anzahl der weißen Kugeln.
\(n\), die Anzahl der Kugeln, die als Stichprobe gezogen wird. Hier ist \(n=4\).

Wenn wir unser Beispiel mit der Zufallsvariablen \(X\) beschreiben, sieht die hypergeometrische Verteilung wie folgt aus:

\[ X \sim \text{HG}(15, 5, 4) \]

Träger

Die hypergeometrische Verteilung hat denselben Träger wie die Binomialverteilung: Wenn man \(n=4\) Kugeln zieht, sind 0 bis 4 Erfolge möglich. Allgemein ist also

\[ \mathcal{T} = \{ 0, 1, \ldots, n \} \]

Dichte

Die Dichte einer hypergeometrisch verteilten Zufallsvariable \(X\) lautet

\[ f(x) = \frac{{M \choose x} {N-M \choose n-x}}{N \choose n} \]

In unserem Beispiel ist also die Wahrscheinlichkeit, bei 4 gezogenen Kugeln 2 weiße Kugeln darunter zu finden, gleich

\[ f(2) = \frac{{5 \choose 2} {15-5 \choose 4-2}}{15 \choose 4} = 0.3297 \]

Die Dichte \(f(x)\) für die hypergeometrische Verteilung unseres Beispiels.

Beachte hier, dass die Werte \(N\), \(M\) und \(n\) das Experiment beschreiben, und dann (gegeben einem Experiment) nicht mehr verändert werden. Die Variable \(x\) hingegen kann alle möglichen Ausgänge des Experiments annehmen, hier also alles von 0 bis 4.

Verteilungsfunktion

Für die Verteilungsfunktion gibt es hier, wie bei der Binomialverteilung, keine kürzere Formel, sondern man summiert einfach die Dichte über alle möglichen Ausprägungen aus:

\[ F(x) = \mathbb{P}(X \leq x) = \sum_{k=0}^x f(k) \]

Die Verteilungsfunktion \(F(x)\) für dieses Beispielexperiment.

Möchte ich also die Wahrscheinlichkeit wissen, höchstens drei weiße Kugeln in meiner Stichprobe zu erhalten, muss ich die einzelnen Wahrscheinlichkeiten aufsummieren:

\[\begin{align*} F(3) = \mathbb{P}(X \leq 3) &=\mathbb{P}(X=0) +\mathbb{P}(X=1)+\mathbb{P}(X=2)+\mathbb{P}(X=3) \\&= 0.1538 + 0.4396 + 0.3297 + 0.0733 \\&= 0.996 \end{align*}\]

Einen Trick gibt es allerdings in den Fällen, in denen man viele einzelne Wahrscheinlichkeiten im Taschenrechner berechnen müsste: Über die Gegenwahrscheinlichkeit lässt sich derselbe Wert viel schneller berechnen:

\[F(3) = \mathbb{P}(X \leq 3) = 1-\mathbb{P}(X=4) = 1-0.004 = 0.996\]

Erwartungswert

Der Erwartungswert ist, analog zur Binomialverteilung, einfach \(n\)-mal der anfängliche Anteil an Treffern, also \(M/N\). Es ist daher

\[ \mathbb{E}(X) = n \cdot \frac{M}{N} \]

Varianz

Die Varianz berechnet man durch

\[ \mathbb{V}(X) = n \frac{M}{N} \left( 1-\frac{M}{N} \right) \frac{N-n}{N-1} \]

Beispielaufgabe

Mit Hilfe der hypergeometrischen Verteilung können wir zum Beispiel die folgenden Fragen beantworten:

Wie hoch ist die Wahrscheinlichkeit, beim deutschen Lotto (6 aus 49) drei gerade und drei ungerade Zahlen zu ziehen?
Wie hoch ist dort die Wahrscheinlichkeit für sechs gerade Zahlen?

In beiden Fragen verwenden wir eine Zufallsvariable mit der Verteilung

\[ X \sim \text{HG}(49, 24, 6). \]

Denn es gibt insgesamt \(N=49\) Kugeln, davon sind \(M=24\) eine gerade Zahl, und wir ziehen \(n=6\) dieser Kugeln. Mit der Dichtefunktion für diese Verteilung können wir nun die Wahrscheinlichkeit für drei (über \(f(3)\)), sechs (über \(f(6)\)), oder beliebig viele Kugeln mit geraden Zahlen bestimmen:

\[\begin{align*} f(3) &=\frac{{24 \choose 3} {49-24 \choose 6-3}}{49 \choose 6} = 0.3329 \\f(6) &=\frac{{24 \choose 6} {49-24 \choose 6-6}}{49 \choose 6} = 0.0096 \end{align*}\]

Der Satz von Bayes

5 Antworten

Der Satz von Bayes ist eine hilfreiche Regel, um bedingte Wahrscheinlichkeiten der Form \(\mathbb{P}(A|B)\) auszurechnen, wenn nur „andersherum“ bedingte Wahrscheinlichkeiten der Form \(\mathbb{P}(B|A)\) gegeben sind.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Herleitung des Satzes von Bayes

Der Satz von Bayes erweitert die bekannte Formel für bedingte Wahrscheinlichkeiten:

\[ \mathbb{P}(A|B) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)} \]

Falls die im Zähler stehende gemeinsame Wahrscheinlichkeit nicht gegeben ist, kann man sie auch durch den Multiplikationssatz bestimmen:

\[ \mathbb{P}(A \cap B) =\mathbb{P}(A | B) \cdot\mathbb{P}(B)\]

Diese Regel ergibt sich durch das Umstellen der Formel für die bedingte Wahrscheinlichkeit. Da in der Notation die Reihenfolge bei zwei gemeinsam eintretenden Ereignissen egal ist, d.h. \(\mathbb{P}(A \cap B) = \mathbb{P}(B \cap A)\), gilt der Multiplikationssatz auch mit umgekehrten Buchstaben:

\[ \mathbb{P}(A \cap B) =\mathbb{P}(B | A) \cdot\mathbb{P}(A)\]

Genau diese Formel wird nun im Zähler ersetzt, und man erhält den Satz von Bayes:

\[ \mathbb{P}(A|B) = \frac{\mathbb{P}(B | A) \cdot\mathbb{P}(A)}{\mathbb{P}(B)} \]

Falls \(\mathbb{P}(B)\) nicht gegeben ist

In manchen Aufgaben ist die Wahrscheinlichkeit \(\mathbb{P}(B)\) im Nenner nicht gegeben. Dann muss man sie über einen Umweg mit dem Satz der totalen Wahrscheinlichkeit herleiten.

Für den Spezialfall von nur zwei Aufteilungen von \(A\) ersetzt man den Nenner also wie folgt:

\[ \mathbb{P}(A|B) = \frac{\mathbb{P}(B | A) \cdot\mathbb{P}(A)}{\mathbb{P}(B|A) \cdot \mathbb{P}(A) +\mathbb{P}(B|\bar{A}) \cdot \mathbb{P}(\bar{A})} \]

Beispielaufgabe

Eine neu entwickelte Maschine kann gefälschte Geldscheine erkennen. Wir definieren das Ereignis \(A\): „Die Maschine schlägt Alarm“, und Ereignis \(F\): „Der Geldschein ist falsch“.

Wir möchten nun herausfinden, wie hoch die Wahrscheinlichkeit ist, dass ein Geldschein tatsächlich eine Fälschung ist, gegeben die Maschine schlägt Alarm. Gesucht ist also

\[ \mathbb{P}(F|A). \]

Die Maschine wurde anhand vieler echter und unechter Scheine getestet. Man fand heraus, dass die Maschine bei einem falschen Schein mit 96% Sicherheit Alarm schlägt. Allerdings gibt die Maschine auch bei 1% der echten Geldscheine Alarm. Wir wissen also:

\(\mathbb{P}(A|F) = 0.96\)
\(\mathbb{P}(A|\bar{F}) = 0.01\)

Zusätzlich ist bekannt, dass 0,01% aller im Umlauf befindlichen Geldscheine Fälschungen sind. Das heißt:

\(\mathbb{P}(F) = 0.0001\)

Aufgaben dieser Art lassen sich mit dem Satz von Bayes lösen, da \(\mathbb{P}(A|F)\) gegeben, aber \(\mathbb{P}(F|A)\) gesucht ist. Wir starten also mit der Formel von Bayes (adaptiert mit den Buchstaben für unsere Ereignisse):

\[ \mathbb{P}(F|A) = \frac{\mathbb{P}(A|F) \cdot\mathbb{P}(F)}{\mathbb{P}(A)} \]

Die beiden Faktoren im Zähler sind in der Aufgabe gegeben, wir können sie also einfach einsetzen: \(\mathbb{P}(A|F) = 0.96\) und \(\mathbb{P}(F) = 0.0001\).

Im Nenner fehlt uns noch \(\mathbb{P}(A)\), die nicht-bedingte Wahrscheinlichkeit, dass die Maschine Alarm schlägt. Diese Wahrscheinlichkeit ist nicht gegeben, aber wir haben die beiden bedingten Wahrscheinlichkeiten, dass die Maschine Alarm schlägt, gegeben der Geldschein ist echt bzw. falsch. Wir können \(\mathbb{P}(A)\) also mit dem Satz der totalen Wahrscheinlichkeit berechnen:

\[ \begin{align*}\mathbb{P}(A) &=\mathbb{P}(A|F)\cdot \mathbb{P}(F) +\mathbb{P}(A|\bar{F})\cdot \mathbb{P}(\bar{F}) \\ &= 0.96 \cdot 0.0001 + 0.01 \cdot 0.9999 \\ &= 0.010095 \end{align*} \]

Die Maschine schlägt also insgesamt in etwas über 1% aller Fälle Alarm. Mit diesem Wert können wir nun die gesuchte bedingte Wahrscheinlichkeit berechnen, dass ein Geldschein gefälscht ist, gegeben die Maschine schlägt Alarm:

\[ \mathbb{P}(F|A) = \frac{\mathbb{P}(A|F) \cdot\mathbb{P}(F)}{\mathbb{P}(A)} = \frac{0.96 \cdot 0.0001}{0.010095} = 0.0095\]

Dieser Wert ist erschreckend: Wenn die Maschine Alarm schlägt, ist der betreffende Geldschein nur zu etwa 0,95% eine Fälschung, und umgekehrt zu etwa 99,05% ein echter Geldschein.

Dieses Phänomen lässt sich dadurch erklären, dass sich sehr viel mehr echte als falsche Geldscheine im Umlauf befinden, und dass also ein Alarm viel wahrscheinlicher fälschlicherweise bei einem echten Geldschein gegeben worden ist als korrekterweise bei einem gefälschten Schein. Um eine verlässliche Maschine zu bauen, muss man also entweder die Wahrscheinlichkeit für einen Fehlalarm senken, oder die Genauigkeit beim tatsächlichen Erkennen gefälschter Scheine erhöhen.

Klausuraufgabe

Die Rot-Grün-Blindheit ist eine angeborene Sehschwäche, die bei etwa 9% aller Jungen, aber nur bei 0,6% aller Mädchen auftritt. Wir nehmen hier an, dass ein neugeborenes Kind zu 51% ein Junge wird, und zu 49% ein Mädchen.

Eine Mutter erzählt dir, dass ihr Kind eine Rot-Grün-Blindheit hat. Bestimme nun die Wahrscheinlichkeit, gegeben dieser Information, dass es sich um einen Jungen handelt.

Hinweis: Gesucht ist die Wahrscheinlichkeit \(\mathbb{P}(J | B)\), mit den Ereignissen \(J\)=“Kind ist ein Junge“ (d.h. \(\bar{J}\)=“Kind ist ein Mädchen“) und \(B\)=“Kind hat Rot-Grün-Blindheit“. Verwende den Satz von Bayes, um diese Wahrscheinlichkeit zu ermitteln. Auf dem Weg dorthin begegnest du \(\mathbb{P}(B)\), der Wahrscheinlichkeit, dass irgendein Kind unter der Rot-Grün-Blindheit leidet. Das ermittelst du mit dem Satz der totalen Wahrscheinlichkeit.

Lösung (klick)

Gegeben sind in dieser Aufgabe die folgenden Wahrscheinlichkeiten:

\(\mathbb{P}(B|J) = 0.09\)
\(\mathbb{P}(B|\bar{J}) = 0.006\)
\(\mathbb{P}(J) = 0.51\)
\(\mathbb{P}(\bar{J}) = 0.49\)

Die gesuchte Wahrscheinlichkeit \(\mathbb{P}(J|B)\) erhalten wir wieder über den Satz von Bayes:

\[ \mathbb{P}(J|B) = \frac{\mathbb{P}(B|J) \cdot\mathbb{P}(J)}{\mathbb{P}(B)} \]

Bis auf \(\mathbb{P}(B)\) können wir alle Werte direkt einsetzen. Für \(\mathbb{P}(B)\) verwenden wir den Satz der totalen Wahrscheinlichkeit:

\[ \mathbb{P}(B) =\mathbb{P}(B|J) \cdot \mathbb{P}(J) +\mathbb{P}(B|\bar{J}) \cdot \mathbb{P}(\bar{J}) = 0.09 \cdot 0.51 + 0.006 \cdot 0.49 = 0.04884 \]

Damit erhalten wir die gesuchte Wahrscheinlichkeit:

\[ \mathbb{P}(J|B) = \frac{\mathbb{P}(B|J) \cdot\mathbb{P}(J)}{\mathbb{P}(B)} = \frac{0.09 \cdot 0.51}{0.04884} = 0.9398 \]

Das Kind ist also zu etwa 94% ein Junge, wenn man die Information hat, dass es rot-grün-blind ist.

Anleitung zum Rechnen mit Wahrscheinlichkeiten

4 Antworten

Das Umgehen mit Wahrscheinlichkeiten gehört zum essentiellen Handwerkszeug in den einführenden Statistikklausuren. Die wichtigsten Regeln, die verwendet werden, wurden in früheren Artikeln bereits besprochen:

Laplace-Wahrscheinlichkeit	\(\mathbb{P}(A) =\frac{\text{Anzahl der }\mathrm{f\ddot{u}r }A\text{ „}\mathrm{g\ddot{u}nstige}\text{“ Ergebnisse}}{\text{Anzahl aller } \mathrm{m\ddot{o}glichen}\text{ Ergebnisse}}\)
Bedingte Wahrscheinlichkeit	\(\mathbb{P}(A\|B) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)}\)
Totale Wahrscheinlichkeit	\(\mathbb{P}(A) =\mathbb{P}(A \| B) \cdot \mathbb{P}(B) +\mathbb{P}(A \| \bar{B}) \cdot \mathbb{P}(\bar{B})\)
Multiplikationssatz	\(\mathbb{P}(A \cap B) =\mathbb{P}(A \| B) \cdot\mathbb{P}(B)\)
Multiplikationssatz für unabhängige Ereignisse	\(\mathbb{P}(A \cap B) =\mathbb{P}(A) \cdot\mathbb{P}(B)\)
Satz von Bayes	\(\mathbb{P}(A\|B) = \frac{\mathbb{P}(B \| A) \cdot\mathbb{P}(A)}{\mathbb{P}(B)}\)

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Welche Formel man in einer bestimmten Situation braucht, kann man herausfinden, indem man die Aufgabe systematisch angeht:

Benenne die Ereignisse und Wahrscheinlichkeiten der Aufgabe mit Buchstaben, falls noch keine gegeben sind.
Notiere in Formelschreibweise, was gesucht ist (z.B.: \(\mathbb{P}(B|C)\)).
Notiere in Formelschreibweise, welche Werte gegeben sind.
Suche die Formeln heraus, in denen sowohl die gesuchten als auch die gegebenen Werte vorkommen.

Dazu ist es hilfreich, noch ein paar zusätzliche Regeln zu kennen (wenn sie nicht schon offensichtlich sind):

\(\mathbb{P}(\bar{A}) = 1-\mathbb{P}(A)\). Mit \(\bar{A}\) ist die Gegenwahrscheinlichkeit von \(A\) gemeint. Das ist natürlich genau die Wahrscheinlichkeit, die auf die Gesamtsumme von 1 fehlt, denn \(\mathbb{P}(A) + \mathbb{P}(\bar{A}) = 1\).
\(\mathbb{P}(A \cup B) =\mathbb{P}(A)+\mathbb{P}(B) -\mathbb{P}(A \cap B)\). Die Wahrscheinlichkeit \(\mathbb{P}(A \cup B)\), dass also entweder \(A\) oder \(B\) eintritt (oder auch beide Ereignisse gleichzeitig), ist deren Summe, minus der Wahrscheinlichkeit dass beide Ereignisse eintreten. Diese Formel kann man sich an einem Venn-Diagramm gut selbst herleiten.

Ab und zu muss man mit den gegebenen Werten erst ein Zwischenergebnis berechnen, bevor man das letztendliche Ergebnis erhalten kann. Das ist zum Beispiel beim Satz von Bayes der Fall, wo man im Nenner die Wahrscheinlichkeit \(\mathbb{P}(A)\) erst über den Satz der totalen Wahrscheinlichkeit berechnen muss. Die folgende Beispielaufgabe illustriert dieses Vorgehen:

Beispielaufgabe

In einer Spielwarenfabrik stehen drei Maschinen 1, 2, und 3, die mit unterschiedlicher Geschwindigkeit Spielzeugsoldaten herstellen. Jede Maschine produziert mit einer bestimmten Wahrscheinlichkeit ein fehlerhaftes Spielzeug, das in der Qualitätskontrolle aussortiert werden muss:

Maschine	1	2	3
Anteil an der Gesamtproduktion	0.15	0.40	0.45
Anteil fehlerhafter Soldaten	0.10	0.02	0.01

Man sieht, dass die Maschine 1 ein älteres Stück ist, das langsamer und fehleranfälliger arbeitet.

Angenommen, man hält nun einen fehlerhaften Spielzeugsoldaten in der Hand. Wie hoch ist die Wahrscheinlichkeit, dass er von Maschine 1 kommt?

Lösungsansatz

Um diese Aufgabe zu lösen, gehen wir wie oben beschrieben Schritt für Schritt vor. Zuerst stellen wir die Aufgabe in Formelschreibweise dar:

Ereignisse benennen: Die Ereignisse „Ein Soldat wurde von Maschine 1 produziert“ können wir einfach \(M_1\), \(M_2\), und \(M_3\) nennen. Das Ereignis „Ein produzierter Soldat ist fehlerhaft“ nennen wir \(F\), somit ist das Ereignis „Ein Soldat ist in Ordnung“ das Gegenereignis \(\bar{F}\).
Gesuchter Wert: Gesucht ist die Wahrscheinlichkeit, dass ein Soldat von Maschine 1 produziert wurde, gegeben er ist fehlerhaft, also: \(\mathbb{P}(M_1|F)\).
Gegebene Werte: Gegeben sind zum Einen die A-priori-Wahrscheinlichkeiten, dass ein beliebiger Soldat von Maschine 1, 2, bzw. 3 kommt. Das sind einfach die Werte \(\mathbb{P}(M_1)=0.15\), \(\mathbb{P}(M_2)=0.40\) und \(\mathbb{P}(M_3)=0.45\). Zusätzlich sind die Anteile fehlerhafter Soldaten die bedingte Wahrscheinlichkeit für \(F\), gegeben der Maschine, also \(\mathbb{P}(F|M_1)=0.10\), \(\mathbb{P}(F|M_2)=0.02\), und \(\mathbb{P}(F|M_3)=0.01\).
Hilfreiche Formeln: Wir sehen, dass eine bedingte Wahrscheinlichkeit gesucht ist, und die „andersrum“ bedingten Wahrscheinlichkeiten gegeben sind. Das sind Aufgabentypen, die mit dem Satz von Bayes gelöst werden können:
\[ \mathbb{P}(A|B) = \frac{\mathbb{P}(B|A)\mathbb{P}(A)}{\mathbb{P}(B)} \]

In dieser Aufgabe beginnen wir also mit dem Satz von Bayes und unseren Ereignissen:

\[ \mathbb{P}(M_1|F) = \frac{\mathbb{P}(F|M_1)\mathbb{P}(M_1)}{\mathbb{P}(F)} \]

Alle diese Werte sind aus der Angabe bekannt, bis auf \(\mathbb{P}(F)\), die Wahrscheinlichkeit, dass ein beliebiger Soldat fehlerhaft ist. Um diese Wahrscheinlichkeit aus den gegebenen Werten zu berechnen, bietet sich der Satz der totalen Wahrscheinlichkeit an:

\[\begin{align*} \mathbb{P}(F) &=\mathbb{P}(F|M_1)\mathbb{P}(M_1) +\mathbb{P}(F|M_2)\mathbb{P}(M_2) +\mathbb{P}(F|M_3)\mathbb{P}(M_3) \\ &= 0.10 \cdot 0.15 + 0.02 \cdot 0.40 + 0.01 \cdot 0.45 \\&= 0.0275 \end{align*}\]

Es sind also insgesamt etwa 2,75% aller Soldaten fehlerhaft. Diesen Wert können wir nun in die Bayes-Formel einsetzten, um die gesuchte Wahrscheinlichkeit zu erhalten:

\[ \mathbb{P}(M_1|F) = \frac{\mathbb{P}(F|M_1)\mathbb{P}(M_1)}{\mathbb{P}(F)} = \frac{0.10 \cdot 0.15}{0.0275} = 0.545 \]

Ein beliebiger defekter Soldat kommt also mit einer Wahrscheinlichkeit von über 50% von Maschine 1. Obwohl diese Maschine nur 15% aller Soldaten produziert, kommen mehr als die Hälfte aller defekten Soldaten von ihr.

Unabhängigkeit von Ereignissen

4 Antworten

Wenn zwei Ereignisse \(A\) und \(B\) voneinander abhängig sind, dann liefert das Eintreten von \(A\) hilfreiche Information über die Wahrscheinlichkeit des Eintretens von \(B\). Dazu zwei Bespiele:

Die Augenfarbe und Haarfarbe einer Person sind voneinander abhängig. Wenn ich z.B. weiß, dass Ereignis \(A\): „eine Person hat schwarze Haare“, eingetreten ist, dann macht das das Ereignis \(D\): „diese Person hat braune Augen“, viel wahrscheinlicher als wenn sie blonde Haare hätte. In diesen Beispiel ist \(A\) von \(D\) abhängig (und umgekehrt auch \(D\) von \(A\)).

Ein Beispiel für zwei unabhängige Ereignisse wäre das Ereignis \(A\): „Eine Person hat schwarze Haare“ und das Ereignis \(C\): „Diese Person ist über 1,70m groß“. Oder, wenn man es auf die Spitze treiben will: das Ereignis \(A\): „eine Person hat schwarze Haare“ und Ereignis \(B\): „Gestern hat es geschneit“ sind ganz bestimmt voneinander unabhängig.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Sobald man mehr als ein Ereignis betrachtet, ist es essentiell zu wissen ob diese Ereignisse voneinander abhängig sind oder nicht. Die Unabhängigkeit zweier Ereignisse ist ein wichtiges Konzept, da sie viele Berechnungen immens vereinfacht. Sind zum Beispiel zwei Ereignisse voneinander unabhängig, kann man ihre gemeinsame Wahrscheinlichkeit viel einfacher berechnen als wenn sie abhängig sind.

Vereinfachungen wenn zwei Ereignisse unabhängig sind

Wenn zwei Ereignisse voneinander unabhängig sind, ist die bedingte Wahrscheinlichkeit gleich der unbedingten Wahrscheinlichkeit:
\[ \mathbb{P}(A|B) = \mathbb{P}(A) \] Dieses Gesetz gilt auch umgekehrt:
\[ \mathbb{P}(B|A) = \mathbb{P}(B) \] Das leuchtet ein, da das Eintreten von \(B\) keine genauere Information über das Eintreten von \(A\) (oder umgekehrt) liefert. Um auf das oben aufgeführte Beispiel zurückzugreifen: Die bedingte Wahrscheinlichkeit dass eine Person schwarze Haare hat, gegeben es hat gestern geregnet, ist genau gleich der unbedingten Wahrscheinlichkeit, dass eine Person schwarze Haare hat. Die Tatsache dass es gestern geregnet hat, liefert keine zusätzliche Information. (Anders wäre es mit Ereignis \(D\): „diese Person hat braune Augen“. Das wäre eine hilfreiche Information.)
Außerdem kann man bei zwei unabhängigen Ereignissen die gemeinsame Wahrscheinlichkeit für das Eintreten beider Ereignisse einfach durch das Produkt der einzelnen Wahrscheinlichkeiten berechnen:
\[ \mathbb{P}(A \cap B) = \mathbb{P}(A) \cdot \mathbb{P}(B) \] Falls zwei Ereignisse abhängig sind, gilt diese Formel nicht, sondern man verwendet in einem der beiden Faktoren die bedingte Wahrscheinlichkeit:
\[ \mathbb{P}(A \cap B) = \mathbb{P}(A|B) \cdot \mathbb{P}(B) \] Für unabhängige \(A\) und \(B\) reduziert sich der erste Faktor zur unbedingten Wahrscheinlichkeit, da in diesem Fall \(\mathbb{P}(A|B) = \mathbb{P}(A)\) gilt.

Der Satz der totalen Wahrscheinlichkeit

3 Antworten

Mit dem Satz der totalen Wahrscheinlichkeit kann man die Wahrscheinlichkeit für ein Ereignis \(A\) berechnen, wenn man nur bedingte oder gemeinsame Wahrscheinlichkeiten abhängig von einem zweiten Ereignis \(B\) gegeben hat.

Klausuraufgaben

Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Als Beispiel sei hier die Parkinson-Krankheit genannt. Da mehr Männer als Frauen an Parkinson erkranken, sind hauptsächlich geschlechtsspezifische Zahlen veröffentlicht. Möchte man aber die Wahrscheinlichkeit der Erkrankung für eine zufällige Person unabhängig vom Geschlecht bestimmen, braucht man dafür den Satz der totalen Wahrscheinlichkeit. Mit Hilfe der Erkrankungsrate pro Geschlecht, dem Verhältnis von Frauen und Männern in der Gesamtbevölkerung, und der entsprechenden Formel erhält man dann die Gesamtwahrscheinlichkeit einer Parkinsonerkrankung.

In einem Venn-Diagramm kann man das Aufteilen einer totalen Wahrscheinlichkeit wie folgt illustrieren:

Es ist also

\[\mathbb{P}(A) = \mathbb{P}(A \cap B) + \mathbb{P}(A \cap \bar{B}). \]

In unserem Beispiel der Parkinson-Krankheit hieße das: Die Wahrscheinlichkeit für eine beliebige Person, an Parkinson zu erkranken, setzt sich zusammen als die Summe der Wahrscheinlichkeit, ein Mann zu sein und an Parkinson zu erkranken, plus die Wahrscheinlichkeit, eine Frau zu sein und an Parkinson zu erkanken.

Meist sind nicht die gemeinsamen Wahrscheinlichkeiten \(\mathbb{P}(A \cap B)\), sondern die bedingten Wahrscheinlichkeiten \(\mathbb{P}(A | B)\) gegeben. Man kann die gemeinsamen Wahrscheinlichkeiten aber erhalten, indem man die Formel der bedingten Wahrscheinlichkeiten etwas umstellt:

\[ \mathbb{P}(A \cap B) = \mathbb{P}(A | B) \cdot \mathbb{P}(B) \]

Wir erhalten also die verbreitetste Version der Formel für die totale Wahrscheinlichkeit:

\[\mathbb{P}(A) =\mathbb{P}(A | B) \cdot \mathbb{P}(B) +\mathbb{P}(A | \bar{B}) \cdot \mathbb{P}(\bar{B}). \]

Je nachdem, ob in einer Aufgabe die bedingten oder die gemeinsamen Wahrscheinlichkeiten gegeben sind, nimmt man die eine oder andere dieser beiden Formeln. In den allermeisten Fällen arbeitet man aber mit bedingten Wahrscheinlichkeiten.

Beispielaufgabe

Mit dieser Formel können wir nun für eine zufällige Person beliebigen Geschlechts die totale Wahrscheinlichkeit berechnen, an Parkinson zu erkranken. Wir benötigen dazu die folgenden Notationen:

\(A\): Die Person erkrankt an Parkinson
\(B\): Die Person ist männlich.
\(\bar{B}\): Das Gegenteil von \(B\), also: Die Person ist weiblich.

Aus einer Onlinepublikation über die Prävalenz von Parkinson erhalten wir die folgenden Wahrscheinlichkeiten:

Die Wahrscheinlichkeit für einen Mann, an Parkinson zu erkranken, liegt bei 0,309%. In unserer Formel bedeutet das: \(\mathbb{P}(A|B) = 0.00309\).
Die Wahrscheinlichkeit für eine Frau, an Parkinson zu erkranken, liegt bei 0,241%. Analog dazu: \(\mathbb{P}(A|\bar{B}) = 0.00241\).
Es gibt minimal mehr Männer in der Gesamtbevölkerung, nämlich 51,1%. Also: \(\mathbb{P}(B) = 0.511\).

Mit diesen Werten können wir nun die Gesamtwahrscheinlichkeit für eine beliebige Person berechnen:

\[\begin{array}{rclcl} \mathbb{P}(A) & = & \mathbb{P}(A | B) \cdot \mathbb{P}(B) +\mathbb{P}(A | \bar{B}) \cdot \mathbb{P}(\bar{B}) = \\ & & 0.00309 \cdot 0.511 + 0.00241 \cdot 0.489 = \\ & & 0.00275748 \end{array}\]

Wir enden also bei einer Wahrscheinlichkeit von 0,276% für eine Person beliebigen Geschlechts, an Parkinson zu erkranken. Wichtig ist hier, dass das nicht genau der Mittelwert zwischen \(\mathbb{P}(A|B) = 0.00309\) und \(\mathbb{P}(A|\bar{B}) = 0.00241\) ist, sondern dass diese Werte mit dem Geschlechterverhältnis gewichtet werden, das zwar nahe an 50/50 liegt, aber eben nicht genau gleich ist.

Mehr als zwei Gruppen in \(B\)

Man kann die totale Wahrscheinlichkeit auch bestimmen, wenn es sich um mehr als zwei Gruppen handelt. Dann arbeitet man nicht mit den beiden Ereignissen \(B\) und \(\bar{B}\), sondern z.B. mit drei Ereignissen \(B_1\), \(B_2\), und \(B_3\). Wichtig ist hier, dass diese Gruppen disjunkt sind, d.h. dass sie sich nicht überschneiden. Die Folge dieser Voraussetzung ist, dass sich ihre Wahrscheinlichkeiten zu 1 summieren, dass also jedes mögliche Ereignis in eines, und genau eines der drei Unterereignisse fällt:

\[ \mathbb{P}(B_1) +\mathbb{P}(B_2) +\mathbb{P}(B_3) = 1 \]

Für drei Untergruppen (und analog auch für beliebig viele Untergruppen) des Ereignisses \(B\) bestimmt man die totale Wahrscheinlichkeit wie folgt:

\[ \begin{array}{rclcl} \mathbb{P}(A) & = & \mathbb{P}(A|B_1)\cdot \mathbb{P}(B_1) + \\ & &\mathbb{P}(A|B_2)\cdot \mathbb{P}(B_2) + \\ & &\mathbb{P}(A|B_3)\cdot \mathbb{P}(B_3) \end{array} \]