Mit Hilfe von bedingten Wahrscheinlichkeiten kann man die Wahrscheinlichkeit für ein Ereignis genauer bestimmen, wenn zusätzliche Information vorhanden ist. Diese zusätzliche Information ist ein anderes Ereignis, das schon eingetreten ist, und wodurch wir nun eine genauere Einschätzung der Wahrscheinlichkeit haben.
Dazu ein Beispiel: Möchten wir an einem Junitag die Wahrscheinlichkeit \(\mathbb{P}(A)\) bestimmen, dass morgen ein sonniger Tag wird, können wir zum Beispiel das Wetter an allen Junitagen der letzten zehn Jahre anschauen, und abzählen, an wievielen dieser Tage die Sonne schien. Wir können aber eine genauere Aussage über diese Wahrscheinlichkeit machen, wenn wir zusätzlich wissen dass es heute stark regnet. Wenn wir das Ereignis „Heute regnet es“ mit dem Buchstaben \(B\) bezeichnen, können wir die Wahrscheinlichkeit dass es morgen sonnig wird, gegeben heute regnet es stark, ausdrücken durch
\[ \mathbb{P}(A|B). \]
Man spricht diese Schreibweise aus als „Die Wahrscheinlichkeit von \(A\), gegeben \(B\)“.
Veranschaulichung an Venn-Diagrammen
Die Tatsache, dass man durch die Kenntnis des Eintretens von Ereignis \(B\) eine genauere Aussage über die Wahrscheinlichkeit des Eintretens von \(A\) machen kann, kann man mit Hilfe eines Venn-Diagramms veranschaulichen. Wenn wir wissen, dass \(B\) eingetreten ist, reduziert sich der gesamte Ergebnisraum \(\Omega\) auf \(B\):
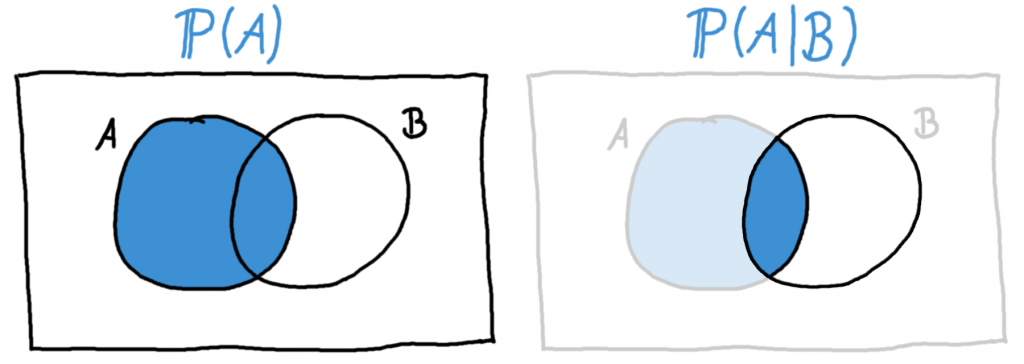
Links: Die Wahrscheinlichkeit für \(A\) ohne zusätzliche Information ist der ausgefüllte Kreis. Rechts: Wissen wir, dass \(B\) eingetreten ist, können wir die Wahrscheinlichkeit für \(A\) gegeben \(B\) berechnen. Die ausgefüllte Fläche in der Mitte ist hier \(A \cap B\).
Die Idee hinter bedingten Wahrscheinlichkeiten ist einfach, aber deren Berechnung kann zu Beginn oft kompliziert sein. Mit etwas Übung ist dieses Thema aber auch leicht zu bewältigen.
Etwas Übung
Sehen wir uns für eine Beispielrechnung die Studenten einer Statistikvorlesung an. Wir beobachten, wieviele der Studenten auf die Klausur lernen bzw. nicht lernen, und wieviele der Studenten die Klausur bestehen. Uns interessiert am Ende die Wahrscheinlichkeit, die Klausur zu bestehen, gegeben man hat auf sie gelernt.
Wir haben insgesamt \(n=50\) Studenten beobachtet. Von ihnen haben 25 auf die Klausur gelernt, und die übrigen 25 haben nicht gelernt. 30 der Studenten haben die Klausur bestanden. Von den 25 Studenten, die nicht auf die Klausur gelernt haben, haben 10 Studenten bestanden, und die übrigen 15 sind durchgefallen.
Erstelle aus diesen Angaben zuerst eine Kreuztabelle der Merkmale \(L\)=“Auf die Klausur gelernt“ und \(B\)=“Klausur bestanden“.
Angenommen, wir nehmen aus dieser Gruppe Studenten nun eine zufällige Person heraus, können wir für sie die Wahrscheinlichkeit \(\mathbb{P}(B)\) bestimmen, dass sie die Klausur bestanden hat. Von 50 Studenten haben 30 die Klausur bestanden:
\[ \mathbb{P}(B) = \frac{30}{50} = 0.6 \]
Wenn wir aber nun zusätzlich wissen, dass diese Person gelernt hat, befinden wir uns nur in der ersten Zeile der obigen Kreuztabelle (vergleiche auch die bedingten Häufigkeiten im Artikel zu Kreuztabellen). Von insgesamt 25 Studenten, die auf die Klausur gelernt haben, haben sie 20 Studenten bestanden. Es ist also
\[ \mathbb{P}(B|L) = \frac{20}{25} = 0.8, \]
und somit ist die Wahrscheinlichkeit, dass der Student bestanden hat, gegeben er hat auf die Klausur gelernt, 80%.
Mathematisch drückt man die obige Formel wie folgt aus:
\[ \mathbb{P}(B|L) = \frac{\mathbb{P}(B \cap L)}{\mathbb{P}(L)} \]
Das ist somit die allgemeine Formel für die bedingte Wahrscheinlichkeit. Meistens werden in einer Formelsammlung natürlich statt \(B\) und \(L\) die Buchstaben \(A\) und \(B\) verwendet, aber das ist nur eine Sache der Notation, und macht sonst keinen Unterschied.
Beispielaufgabe
Wir werfen einen normalen Würfel, und betrachten die Ereignisse \(A\) = „Es kommt eine gerade Zahl“, und \(B\) = „Es kommt eine Zahl kleiner oder gleich 3“.
a) Bestimme die Wahrscheinlichkeit für \(A\).
b) Bestimme die Wahrscheinlichkeit für \(A\), gegeben \(B\) ist bereits eingetreten.

 Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zuerst ein Lob, ganz fantastische Aufbereitung.
Doch beim letzten Beispiel hier frage ich warum die Chancen für eine Einzelziffer in dieser Berechnung dann größer ist, als die normale, wenn nur 1 Zahl erwartet wird. Also x aus 6 = 1/6. Warum aber mit den Parametern sich die Wahrscheinlichkeit verdoppelt versteh ich nicht.
Weil es nicht mehr „aus 6“, sondern nun „aus 3“ (eine von 4, 5, oder 6) ist.
VG,
Alex
Hallo lieber Alex, ist es nicht so, dass es eine von (1,2 oder 3) ist? Dachte durch die Info, dass B kleiner oder gleich drei ist, beschränken wir uns also auf dessen Menge. Habe ich das falsch verstanden? Habe auch als Antwortsatz: Mit 1/3 Wahrscheinlichkeit werfen wir eine gerade Zahl, die kleiner gleich 3 ist. Wobei das iwie unsinnig ist, da 3 ja ungerade ist…
Hi,
ja, es ist aus 1, 2, oder 3. Ich weiß nicht mehr warum ich oben 4, 5, 6 geschrieben habe – vielleicht war das ein alter Artikel 🙂
Bei deinem Antwortsatz müsste es wohl 1/6 heißen, denn da kommt nur die gewürfelte 2 in Frage, also eine von 6 Ergebnissen.
VG
Alex
Hallo,
sorry aber das verstehe ich nicht ganz: Eine gerade Zahl (2,4,6) und die zweite Bedingung, dass die Zahl kleiner gleich 3 (1,2,3) ist, ist nachvollziehbar. Da bleibt ja aber nur 2 als Möglichkeit übrig. Wieso ist die Wahrscheinlichkeit dann 1/3 und nicht 1/6???
Und wie verhält es sich, wenn ich nun eine UNgerade Zahl (1,3,5) als erste Bedingung will (ist ja immernoch Wahrscheinlichkeit 1/2), die zweite Bedingung bleibt ebenfalls gleich. Weil dann habe ich ja zwei Möglichkeiten übrig (1 und 3), was ja eine andere Wahrscheinlichkeit geben müsste?
Oder habe ich jetzt einen Denkfehler?
Hi,
weil es eben eine *bedingte* Wahrscheinlichkeit ist. Du weißt schon dass die Zahl kleiner gleich 3 ist. Also steht im Nenner eine 3 und keine 6, weil es nur noch 3 Möglichkeiten gibt.
Gruß,
Alex
Das heißt, ich weiß dass ich keine Zahl aus dem Bereich ab 3 werfen werde quasi? 🙂
Richtig. Das ist der „Bedingung“-Teil aus der bedingten Wahrscheinlichkeit 🙂