Archiv des Autors: Alex

Multiple lineare Regression

28 Antworten

In den bisherigen Artikeln zur Regression ging es nur um die einfache lineare Regression. Hier schauen wir uns nun die multiple lineare Regression an.

Das Wort „multipel“ bedeutet, dass wir nun nicht mehr eine, sondern mehrere Einflussgrößen haben. Wichtig: es gibt mehrere Einflussgrößen. Die Anzahl der Zielgrößen verändert sich nicht, es ist immer noch nur eine Zielgröße.

Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Beispiel

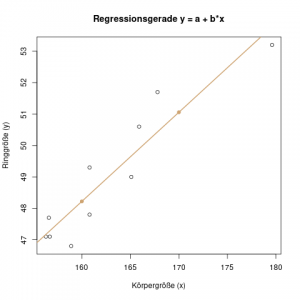
Wir können uns das Beispiel aus den Artikeln zur einfachen linearen Regression ansehen, und es etwas weiterführen. Dort haben wir versucht, mit Hilfe der Regression die Ringgröße \(y\) einer Freundin zu schätzen, gegeben man kennt ihre Körpergröße \(x\).

Wenn dir jetzt allerdings sehr viel daran liegt, eine möglicht exakte Schätzung zu erhalten, um nicht mit einem unpassenden Ring vor ihr zu stehen, kannst du noch mehr Daten sammeln. Beispielsweise zusätzlich zur Körpergröße noch das Gewicht und das Alter von den 10 Frauen, die du befragst.

Die Daten würden nun also um zwei Variablen größer werden, und zum Beispiel so aussehen:

Person \(i\) 1 2 3 4 5 6 7 8 9 10
Körpergröße \(x_1\) 156.3 158.9 160.8 179.6 156.6 165.1 165.9 156.7 167.8 160.8
Körpergewicht \(x_2\) 62 52 83 69 74 52 77 65 79 51
Alter \(x_3\) 24 34 26 51 43 33 22 21 19 34
Ringgröße \(y\) 47.1 46.8 49.3 53.2 47.7 49.0 50.6 47.1 51.7 47.8

Wir haben jetzt nicht mehr eine Einflussgröße \(x\), sondern drei Stück: \(x_1\), \(x_2\), und \(x_3\). Und jede dieser Einflussgrößen hat eine Ausprägung pro Person \(i\). Das heißt, dass nun zwei Zahlen unter dem \(x\) stehen: Eine für die Einflussgröße und eine für die Person. Zum Beispiel ist das Körpergewicht der vierten Person \(x_{2,4} = 69kg\).

Dadurch, dass man jetzt mehr Daten verfügbar hat, kann man eine genauere Schätzung bekommen. Die Regressionsgleichung würde jetzt lauten:

\[ y = a + b_1 x_1 + b_2 x_2 + b_3 x_3 \]

Mit der multiplen Regression kann ich nun Werte für die Parameter \(a\), \(b_1\), \(b_2\), und \(b_3\) erhalten, und mit Hilfe derer kann ich nun wieder eine Vorhersage treffen.

Anmerkung: Genauso wie in der einfachen linearen Regression können die Parameter in anderen Büchern/Skripten anders benannt sein (z.B. \(\beta_0\), \(\beta_1\) usw.). Sie bedeuten aber genau dasselbe.

Schätzung der Parameter

Die Parameterschätzung ist etwas aufwändiger, und von Hand praktisch nicht mehr durchführbar. Grob gesagt werden die drei Einflussgrößen \(x_1\), \(x_2\) und \(x_3\), die man ja als Vektoren ansehen kann, spaltenweise in eine Matrix \(X\) zusammengefasst. Mit Hilfe dieser Matrix und dem Vektor aller Zielgrößen \(y\) kann man dann den Vektor der Parameter (nennen wir ihn mal \(b\)) schätzen:

\[ b = (X^\top X)^{-1} X^\top y \]

Das wird, wie gesagt, etwas komplizierter, und ist auch mit dem Taschenrechner nicht mehr zu lösen. In einer Klausur wird das Berechnen der Parameter in einer multiplen Regression nicht abgefragt werden, weshalb ich die Details hier überspringe. Die Standardliteratur hilft hier aber weiter (ich empfehle die Springer-Bücher zur Regression oder Statistik).

Was aber durchaus Klausurstoff sein kann, ist die Interpretation der Parameter und die Vorhersage mit bereits gegebenen Parametern. Das schauen wir uns jetzt noch genauer an.

Interpretation der Parameter

Wie gesagt, die Berechnung bei der multiplen Regression ist zu kompliziert für Papier und Taschenrechner, daher lasse ich die Herleitung hier weg. Aber mit den Daten aus der obigen Tabelle erhalten wir per Computer gerundet die folgenden Parameter:

\(a=0.6\), \(b_1=0.28\), \(b_2=0.06\), und \(b_3=-0.02\).

Die Regressionsgerade sieht also so aus:

\[ y = 0.66 + 0.28 \cdot x_1 + 0.06 \cdot x_2 – 0.02 \cdot x_3 \]

Was bedeuten diese Parameter nun?

Der Wert \(b_1\), also 0.28, sagt aus, dass bei einer Person, die einen Zentimeter größer ist als eine andere, die Ringgröße im Durchschnitt um 0.28 größer ist. Da der Wert 0.28 größer als Null ist, sprechen wir hier von einem positiven Effekt: Eine größere Körpergröße führt zu einer größeren Ringgröße.

Andersherum ist es beim Alter. Der Wert von -0.02 sagt aus, dass eine Person, die ein Jahr älter ist, im Durchschnitt eine um 0.02 kleinere Ringgröße hat. Das ist ein negativer Effekt, denn der Wert \(b_3\) ist kleiner als Null.

Da wir bei einer Stichprobe aber immer mit zufälligen Daten arbeiten, ist der Parameter für quasi jede Einflussgröße nie exakt Null. Der Parameter für das Alter, die -0.02, sind z.B. so klein, dass sie eventuell schon zufällig auftreten. Die Vermutung liegt nahe, dass das Alter gar keinen Einfluss auf die Ringgröße hat (aber das Gewicht und die Körpergröße durchaus).

Um zu prüfen, ob eine Einflussgröße tatsächlich einen Einfluss hat, gibt statistische Software normalerweise einen \(p\)-Wert zusätzlich zu dem Parameterschätzer aus. Dieser \(p\)-Wert gehört zu der Hypothese, dass der jeweilige Effekt (z.B. vom Alter) gleich Null ist. Wenn der \(p\)-Wert klein genug ist (meist: kleiner als 0.05), dann geht man davon aus, dass die zugehörige Einflussgröße tatsächlich einen Effekt auf die Zielgröße hat, und man spricht von einem signifikanten Effekt.

In unserem Beispiel sind die \(p\)-Werte:
– Für \(b_1\) (Körpergröße): \(p=0.0000026\)
– Für \(b_2\) (Gewicht): \(p=0.00099\)
– Für \(b_3\) (Alter): \(p=0.112\)

Da nur die ersten beiden \(p\)-Werte kleiner als 0.05 sind, können wir hier schlußfolgern, dass sowohl die Körpergröße, als auch das Gewicht einen signifikanten Einfluss auf die Ringgröße haben, aber das Alter nicht.

(Das Berechnen der \(p\)-Werte ist wieder etwas komplizierter, und in einer Klausur wohl nicht gefragt werden, und wird daher hier übersprungen. Falls das jemand genauer wissen will, verweise ich wieder auf die Standardliteratur zur Regression.)

Vorhersage bei der multiplen linearen Regression

Bei der multiplen linearen Regression läuft die Vorhersage genauso ab wie bei der einfachen Regression, nur eben mit mehreren Einflussgrößen. Unsere Regressionsgleichung lautet:

\[ y = 0.66 + 0.28 \cdot x_1 + 0.06 \cdot x_2 – 0.02 \cdot x_3 \]

Das heißt, wenn unsere Freundin nun wie bisher 170cm groß ist, aber wir zusätzlich wissen, dass sie 68kg wiegt und 29 Jahre alt ist, dann können wir eine genauere Schätzung für die Ringgröße abgeben:

\[y = 0.66 + 0.28 \cdot 170 + 0.06 \cdot 68 – 0.02 \cdot 29 = 51.76 \]

Wir erwarten also in etwa eine Ringgröße von 51.76, und sollten daher einen Ring mit einer Größe kaufen, der so nah wie möglich daran liegt (also wahrscheinlich einen der Größe 52).

Einfache lineare Regression

29 Antworten

Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

In diesem Artikel wird nun – aufbauend auf das einführende Beispiel – beschrieben, wie man die Regressionsgerade für unsere Beispieldaten berechnet und einzeichnet. Zur Wiederholung:

Wir möchten die Ringgröße (\(y\)) unserer Freundin schätzen, um sie mit einem Ring zu überraschen. Wir wissen aber nur ihre Körpergröße (\(x\)). Um nun die Ringgröße zu schätzen, sammeln wir 10 Datenpunkte von Freunden und Bekannten, und notieren ihre Körpergröße und Ringgröße:

Person \(i\) 1 2 3 4 5 6 7 8 9 10
Körpergröße \(x\) 156.3 158.9 160.8 179.6 156.6 165.1 165.9 156.7 167.8 160.8
Ringgröße \(y\) 47.1 46.8 49.3 53.2 47.7 49.0 50.6 47.1 51.7 47.8

Wir nennen hier \(y\) die Zielgröße, da ihre Vorhersage unser Ziel ist. Die Körpergröße \(x\) wird allgemein auch Einflussgröße genannt. Es gibt aber noch unzählige andere Namen für die beiden Typen von Variablen. In anderen Quellen wird \(y\) auch häufig Zielvariable, Regressand, Outcome, erklärte Variable oder abhängige Variable (weil sie von \(x\) abhängig ist) genannt. Andere Namen für \(x\) sind Kovariable, Input, Regressor, erklärende Variable oder unabhängige Variable.

Diese Daten können wir nun in ein Streudiagramm einzeichnen, und erkennen sofort, dass größere Frauen tendenziell auch größere Ringe brauchen:

regression-motivation1

Die Regression ist nun eine statistische Methode, um die bestmögliche Gerade zu finden, die man durch diese Daten legen kann. Eine Gerade wird ja definiert durch zwei Parameter \(a\) und \(b\); man kann sie dann darstellen als

\[ y = a + b \cdot x \]

Manchmal sieht man übrigens statt \(a + b \cdot x\) auch \(\alpha + \beta \cdot x\) oder \(\beta_0 + \beta_1 \cdot x\), aber das sind nur andere Namen für dieselben Zahlen.

Berechnung der Parameter \(a\) und \(b\)

Wenn wir also die bestmögliche Gerade finden wollen, die wir durch diese Punktwolke an Daten legen können, ist das gleichbedeutend damit, dass wir die bestmöglichen Werte für \(a\) und \(b\) finden wollen. Und dafür wurden die folgenden beiden Formeln entdeckt:

\[ b = \frac{\sum_{i=1}^n (x_i – \bar{x}) \cdot (y_i – \bar{y})}{\sum_{i=1}^n (x_i – \bar{x})^2} \]

Die Formel für \(a\) ist einfacher, aber wir müssen vorher das Ergebnis für \(b\) berechnen und dort einsetzen:

\[ a = \bar{y} – b\cdot \bar{x} \]

Die Werte \(\bar{x}\) und \(\bar{y}\) sind jeweils die Mittelwerte der gemessenen Daten \(x\) und \(y\).

Eine kürzere Formel für die Berechnung von \(b\)

Die Formel für \(b\) ist recht chaotisch, aber es gibt eine Möglichkeit, sie kürzer darzustellen, während sie immernoch dasselbe Ergebnis liefert:

\[ b = r_{xy} \cdot \frac{s_y}{s_x} \]

Dabei ist \(r_{xy}\) die Pearson-Korrelation zwischen \(x\) und \(y\), und \(s_x\) und \(s_y\) jeweils die Standardabweichung von \(x\) bzw. \(y\). Diese Werte muss man natürlich auch erstmal ausrechnen, so dass diese kürzere Formel insgesamt wahrscheinlich mehr Rechenaufwand bedeutet – außer man hat diese Zwischenergebnisse schon z.B. in einer vorherigen Teilaufgabe der Klausur erhalten und kann sie einfach einsetzen.

Beispielaufgabe

Wir berechnen hier die Werte \(a\) und \(b\) für die obenstehende Tabelle von 10 Personen. Dazu brauchen wir die Mittelwerte von \(x\) und \(y\) als Zwischenergebnisse:

\[ \begin{align*} \bar{x} &= \frac{1}{10} \cdot (156.3+158.9+160.8+179.6+156.6+165.1+165.9+156.7+167.8+160.8) \\ &= \frac{1}{10} \cdot 1628.5 \\ &= 162.85 \end{align*} \]

Genauso erhält man dann auch

\[ \bar{y} = 49.03 \]

Zum Berechnen von \(b\) könnte man nun sofort loslegen, alles in den Taschenrechner einzutippen. Das ist aber anfällig für Leichtsinnsfehler, und oft reicht auch der Platz im Taschenrechner nicht für diese große Formel aus. Ich schlage also vor, in mehreren Schritten vorzugehen:

Bestimmen der Werte \((x_i-\bar{x})\) und \((y_i-\bar{y})\)

Zuerst brauchen wir Zwischenergebnisse, wo wir von jedem Wert den zugehörigen Mittelwert abziehen. Aus der Tabelle

Person \(i\) 1 2 3 4 5 6 7 8 9 10
Körpergröße \(x\) 156.3 158.9 160.8 179.6 156.6 165.1 165.9 156.7 167.8 160.8
Ringgröße \(y\) 47.1 46.8 49.3 53.2 47.7 49.0 50.6 47.1 51.7 47.8

werden also die folgenden Werte berechnet:

Person \(i\) 1 2 3 4 5 6 7 8 9 10
\((x_i-\bar{x})\) -6.55 -3.95 -2.05 16.75 -6.25 2.25 3.05 -6.15 4.95 -2.05
\((y_i-\bar{y})\) -1.93 -2.23 0.27 4.17 -1.33 -0.03 1.57 -1.93 2.67 -1.23

Als Beispiel: Der erste Wert für \((x_i-\bar{x})\) ist einfach \(156.3 – 162.85 = – 6.55\).

Berechnen von \(b\)

Jetzt sind wir nicht weit vom Ergebnis entfernt. Wir brauchen im Zähler der Formel für \(b\) nun für jede Person \(i\) das Produkt der beiden Werte \((x_i-\bar{x})\) und \((y_i-\bar{y})\), für die erste Person also z.B. \((-6.55 \cdot -1.93) = 12.6415\).

Im Nenner der Formel für \(b\) brauchen wir das Quadrat der zweiten Zeile, also wir müssen \((x_i-\bar{x})^2\) berechnen.

Diese Werte berechnen wir nun für alle 10 Personen und können sie (ich runde auf zwei Nachkommastellen) in zwei neue Zeilen der Tabelle einfügen:

Person \(i\) 1 2 3 4 5 6 7 8 9 10
\((x_i-\bar{x})\) -6.55 -3.95 -2.05 16.75 -6.25 2.25 3.05 -6.15 4.95 -2.05
\((y_i-\bar{y})\) -1.93 -2.23 0.27 4.17 -1.33 -0.03 1.57 -1.93 2.67 -1.23
\((x_i-\bar{x}) \cdot (y_i-\bar{y})\) 12.64 8.81 -0.55 69.85 8.31 -0.07 4.79 11.87 13.22 2.52
\((x_i-\bar{x})^2\) 42.90 15.60 4.20 280.56 39.06 5.06 9.30 37.82 24.50 4.20

Und wenn man sich jetzt nochmal die Formel für \(b\) anschaut, sieht man dass wir soweit sind: der Zähler ist die Summe der Werte in der dritten Zeile, und der Nenner die Summe der Werte in der vierten Zeile. Die ergeben sich zu

\[ \sum_{i=1}^n (x_i-\bar{x}) \cdot (y_i-\bar{y}) = 131.39 \]

und

\[ \sum_{i=1}^n (x_i-\bar{x})^2 = 463.2 \]

Somit können wir also \(b\) berechnen:

\[ b =\frac{\sum_{i=1}^n (x_i – \bar{x}) \cdot (y_i – \bar{y})}{\sum_{i=1}^n (x_i – \bar{x})^2} = \frac{131.39}{463.2} = 0.2836 \]

Berechnen von \(a\)

Der Wert \(a\) ist nun mit diesem Ergebnis ganz einfach zu erhalten:

\[ a = \bar{y} – b\cdot \bar{x} = 49.03 – 0.2836 \cdot 162.85 = 2.8457 \]

Einzeichnen der Regressionsgerade

Wir haben also nun die letztendliche Regressionsgerade berechnen können:

\[ y = 2.8457 + 0.2836 \cdot x \]

Um die Gerade dann einzuzeichnen, reicht es, zwei Punkte zu bestimmen, indem wir irgendwelche \(x\)-Werte aussuchen, und die zugehörigen \(y\)-Werte bestimmen. Die \(x\)-Werte sollten sich im Rahmen der „normalen“ Werte der Daten bewegen. Mit Hilfe der Grafik können wir z.B. \(x=160\) und \(x=170\) aussuchen. Dann berechnen wir mit der Formel der Regressionsgeraden die zugehörigen \(y\)-Werte:

\[ 2.8457 + 0.2836 \cdot 160 = 48.22 \]

\[ 2.8457 + 0.2836 \cdot 170 = 51.06 \]

Die Punkte \((160, 48.22)\) und \((170, 51.06)\) können wir nun in das Streudiagramm einzeichnen, und eine Gerade durch die beiden Punkte ziehen:

regression-gerade

Vorhersage bei der einfachen linearen Regression

Bisher haben wir gelernt, wie man die beiden Koeffizienten \(a\) und \(b\) berechnet. Jetzt möchten wir mit Hilfe der Parameter auch für neue Daten \(x\) vorhersagen, welchen Wert für \(y\) wir erwarten.

Das Ziel, das wir mit der Regression erreichen wollen, ist nämlich folgendes: Angenommen es kommt eine neue Person, von der wir nur die Körpergröße \(x=170\) wissen. Was ist dann der Erwartungswert der Ringgröße \(y\)? Wir suchen also \(\mathbb{E}(y|x)\), den bedingten Erwartungswert von \(y\), gegeben man kennt \(x\).

Bei der einfachen linearen Regression gibt es ja nur eine Einflussgröße \(x\). Die Regressionsgerade lautet also

\[ y = a + b\cdot x \]

Um eine Vorhersage für die Zielgröße \(y\) zu erhalten, müssen wir also einfach den zugehörigen Wert für \(x\) in die Gleichung einsetzen. Die Werte für \(a\) und \(b\) haben wir vorher schon berechnet.

Als Beispiel: Im Beispiel aus dem vorherigen Artikel haben wir die Werte \(a=2.8457\) und \(b=0.2836\) bestimmt. Welche Ringgröße ist nun bei deiner Freundin zu erwarten, wenn sie eine Körpergröße von \(x=\)170cm hat? Dafür berechnen wir:

\[ y = a + b\cdot x = 2.8457 + 0.2836 \cdot 170 = 51.06 \]

Ein Ring mit der Größe 51 sollte also gut bei ihr passen.

Es ist hier noch wichtig zu erwähnen, dass wir nur den Erwartungswert von \(y\) vorhersagen. Die Ringgröße wird also nicht exakt 51.06 sein, sondern es gibt immer einen kleinen Fehler, den man im linearen Modell \(\epsilon\) (sprich: Epsilon) nennt. In Wirklichkeit lautet die Regressionsgleichung also

\[ y = a + b \cdot x + \epsilon \]

wobei \(\epsilon\) einen zufälligen und unbekannten Fehler bezeichnet.

Dieser Fehler heißt meistens Residuum, aber man trifft ihn auch manchmal unter den Namen Fehlerterm oder Epsilon an.

Regression: Ein einführendes Beispiel

1 Antwort

Idee der Regression

Das Ziel der Regression ist es, den Wert einer bestimmten Variablen anhand einer oder mehrerer bekannter Werte vorherzusagen.

Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Beispiel

Du möchtest deiner Freundin einen Verlobungsring kaufen. Dummerweise kennst du aber ihre Ringgröße nicht. Es ist natürlich zu verdächtig, sie direkt zu fragen, weil sie dann Verdacht schöpfen könnte.

Du weißt aber, dass kleinere Frauen tendenziell auch kleinere Ringgrößen haben, und nach ihrer Körpergröße kannst du sie ohne Bedenken fragen. Sie ist 170cm groß. Was nun? Kannst du mit dieser Information dein Problem lösen?

Ja! Die lineare Regression hilft dir in dieser Situation!

Du befrägst deinen gesamten weiblichen Bekanntenkreis (10 Personen) nach ihrer Körpergröße und ihrer Ringgröße, und erhältst als Ergebnis die folgenden Daten:

regression-motivation1

Deine Tante Emma ist zum Beispiel \(x=\)165cm groß und trägt Ringgröße \(y=\)49. Sie wird durch den Punkt ca. in der Mitte links repräsentiert.

Das sieht hilfreich aus. Da deine Freundin 170cm groß ist (\(x\)-Achse), hat sie wohl in etwa eine Ringgröße von 52 (\(y\)-Achse). Du kaufst ihr einen Ring in dieser Größe, er passt, sie sagt Ja, und ihr seid glücklich bis an euer Lebensende.

Was hier passiert ist, ist dass du in deinem Kopf eine Regression durchgeführt hast, um mit Hilfe einer bekannten Variablen – ihrer Körpergröße – eine unbekannte Variable, nämlich ihre Ringgröße vorherzusagen.

Die Regression in der Statistik ist nun ein mathematisches Werkzeug, um eine exakte Regel zu bauen, mit der man für jede Körpergröße eine „beste“ Vorhersage für die Ringgröße erhält. In diesem Beispiel würde man also die „beste“ Gerade bestimmen, die durch den oberen Graphen geht:

regression-motivation2

Wie man diese Gerade berechnet, interpretiert, und mit ihr Vorhersagen macht, sehen wir dann in den nächsten Abschnitten. Das grundlegende Problem, und das Vorgehen bei der Lösung des Problems, ist aber genau dasselbe wie in diesem Beispiel beschrieben wurde.

Übersicht Inferenzstatistik / Induktive Statistik

10 Antworten

Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Bisher haben wir uns mit der deskriptiven (oder beschreibenden) Statistik, sowie mit der Wahrscheinlichkeitsrechnung beschäftigt:

  • In der deskriptiven Statistik haben wir eine Stichprobe, und beschreiben ihre Eigenschaften (z.B. Mittelwerte, Varianzen, oder Quantile in einem Boxplot). Wichtig hier: Wir beschreiben nur die Stichprobe. Es werden keine Aussagen über die Grundgesamtheit, aus der die Stichprobe kommt, getroffen.
  • In der Wahrscheinlichkeitsrechnung haben wir eine gegebene Verteilung inklusive aller ihrer Parameter, und möchten die Wahrscheinlichkeit bestimmen, mit der zukünftige Daten bestimmte Werte annehmen.

In der Inferenzstatistik (oft auch induktive oder schließende Statistik genannt) gehen wir nun genau andersrum wie in der Wahrscheinlichkeitsrechnung vor: Wir haben eine Stichprobe gegeben, und möchten mit ihrer Hilfe auf die Parameter der darunterliegenden Verteilung in der Grundgesamtheit schließen.

Die Inferenzstatistik verbindet also die vorhergehenden beiden Teile. Wir berechnen Kennzahlen der Stichprobe (deskriptiv), und schließen dann mit Hilfe der Wahrscheinlichkeitsrechnung auf Eigenschaften in der Grundgesamtheit.

a

In der Wahrscheinlichkeitsrechnung haben wir eine Verteilung gegeben und wollen die Wahrscheinlichkeit für gewisse Daten ausrechnen. In der Inferenzstatistik haben wir Daten gegeben und wollen deren Verteilung (hier: Eine Poissonverteilung mit Parameter \(\lambda=2\)) bestimmen.

Sowohl Hypothesentests als auch Regressionsmodelle kommen aus der Inferenzstatistik. Um in diesem Rahmen Inferenz zu betreiben, muss man zuerst eine den Daten unterliegende Verteilung annehmen. Dazu bedienen sich beide Verfahren statistischer Modelle.

Ein statistisches Modell ist eine (idealisierte) Annahme über das System (meistens: eine bestmmte Verteilung), das einen bestimmten Datensatz generiert hat. Unter der Annahme, dass die Stichprobe zufällig aus der Grundgesamtheit entnommen wurde, gilt dasselbe Modell dann für Stichprobe sowie Grundgesamtheit. Dadurch lässt sich Inferenzstatistik betreiben, und es lassen sich aus der Stichprobe Schlussfolgerungen über die Grundgesamtheit ziehen.

Wie gesagt: zwei große Teilgebiete der Inferenzstatistik sind in den einführenden Statistikveranstaltungen besonders wichtig:

  • Zum einen das Schätzen der genauen Parameter (wie z.B. den Wert \(\lambda=2\) in der oberen Grafik) bzw. Bereiche, in denen der Parameter höchstwahrscheinlich liegt (sogenannter Konfidenzintervalle)
  • Zum anderen das Testen, ob gewisse Parameter einen bestimmten, hypothetischen Wert annehmen.

Beim Schätzen haben wir also keine vorherige Meinung, was der Parameter sein könnte, und berechnen einfach einen höchstwahrscheinlichen Wert aus den Daten, und beim Testen haben wir vorher eine Idee über den Parameter (z.B. behaupten wir, dass \(\lambda=3\) ist), und überprüfen die Plausibilität dieser Behauptung (oder Hypothese) in einem Test.

Chi-Quadrat-Verteilung

Schreibe eine Antwort

Idee

Die \(\chi^2\)-Verteilung wird eigentlich nur für einige Hypothesentests verwendet, insbesondere für den Unabhängigkeitstest für Kontingenztabellen. In der „freien Wildbahn“, also zum Modellieren irgendwelcher erhobenen Daten, trifft man sie quasi nie an. Aus diesem Grund sind viele Details dieser Verteilung (Erwartungswert, Dichte, und Varianz) eher unwichtig – nur die Verteilungsfunktion ist interessant, da mit ihr das 95%-Quantil (die wichtige kritische Schranke für Hypothesentests) bestimmt werden kann.

Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Parameter

Die \(\chi^2\)-Verteilung hat einen Parameter, nämlich die Anzahl der Freiheitsgrade, \(df\). Der Wert für die Anzahl der Freiheitsgrade, also \(df\), ist die Anzahl der Beobachtungen, die in diese Zufallsvariable einfließen. Falls man zum Beispiel eine Kreuztabelle einer Umfrage mit 80 Personen analysiert, ist \(df = 80\). Man notiert eine \(\chi^2\)-verteilte Zufallsvariable \(X\) mit \(df\) Freiheitsgraden als

\[ X \sim \chi^2 (df) \]

t

Dichte- und Verteilungsfunktion der \(\chi^2\)-Verteilung für verschiedene beispielhafte Freiheitsgrade.

Träger

Der Träger der \(\chi^2\)-Verteilung ist \(\mathbb{R}^+\), die positiven reellen Zahlen.

Erwartungswert, Varianz und Dichte

Da mit der \(\chi^2\)-Verteilung eigentlich nie Daten modelliert werden, braucht man eigentlich weder die Dichte, noch den Erwartungswert oder die Varianz kennen. Der Vollständigkeit halber sei sie hier trotzdem genannt: Der Erwartungswert für eine \(\chi^2\)-verteilte Zufallsvariable \(X\) mit \(df\) Freiheitsgraden ist \(\mathbb{E}(X) = df\), und ihre Varianz ist \(\mathbb{V}(X)= 2\cdot df\).

Verteilungsfunktion

Wie oben schon erwähnt, ist für die \(\chi^2\)-Verteilung eigentlich nur die Verteilungsfunktion, und dort auch meistens nur das 95%-Quantil als Spezialfall, interessant.

Die Formel für die Verteilungsfunktion ist sehr aufwändig zu notieren und auszurechnen, weshalb es auch hier eine Verteilungstabelle gibt, an der man die wichtigsten Werte einfach ablesen kann. Auch hier gilt es, einfach ein wenig Übung im Umgang mit der Tabelle zu erhalten, damit man die gewünschten Quantilswerte ohne Zeitverlust und Leichtsinnsfehler richtig und schnell ablesen kann.

Tabelle Chi-Quadrat-Verteilung

2 Antworten

Für die \(\chi^2\)-Verteilung gibt es theoretisch, genauso wie bei der \(t\)-Verteilung, auch eine riesige Tabelle für jede mögliche Anzahl an Freiheitsgraden. Daher sind in den Verteilungstabellen nur die wichtigsten paar Quantile aufgeführt. Am häufigsten verwendet wird dabei das 95%-Quantil, da das die kritische Schranke für einen \(\chi^2\)-Test mit Signifikanzniveau \(\alpha=0.05\) ist. In der Tabelle unten ist die Spalte mit dem 95%-Quantil farbig unterlegt.

Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Haben wir also einen \(\chi^2\)-Test mit 5 Freiheitsgraden, und möchten die kritische Schranke für ein Signifikanzniveau von \(\alpha=0.05\) finden, sehen wir in der Zeile für 5 und der Spalte für 0.95 (das ist 1-0.05) nach. Die folgende Grafik veranschaulicht den Wert, den wir suchen:

a

Ablesebeispiel der \(\chi^2\)-Verteilung mit \(df=5\) Freiheitsgraden. Die Dichte (obere Grafik) hat ab der Stelle \(x=11.07\) noch eine Fläche von 5%. Die Verteilungsfunktion (untere Grafik) an der Stelle \(x=11.07\) hat genau den Wert 0.95.

Quantil (\(1-\alpha\))
\(\downarrow\) Anzahl Freiheitsgrade (\(df\)) 0.05 0.10 0.20 0.30 0.50 0.70 0.80 0.90 0.95 0.99 0.999
1 0.004 0.016 0.064 0.148 0.455 1.074 1.642 2.706 3.841 6.635 10.828
2 0.103 0.211 0.446 0.713 1.386 2.408 3.219 4.605 5.991 9.210 13.816
3 0.352 0.584 1.005 1.424 2.366 3.665 4.642 6.251 7.815 11.345 16.266
4 0.711 1.064 1.649 2.195 3.357 4.878 5.989 7.779 9.488 13.277 18.467
5 1.145 1.610 2.343 3.000 4.351 6.064 7.289 9.236 11.070 15.086 20.515
6 1.635 2.204 3.070 3.828 5.348 7.231 8.558 10.645 12.592 16.812 22.458
7 2.167 2.833 3.822 4.671 6.346 8.383 9.803 12.017 14.067 18.475 24.322
8 2.733 3.490 4.594 5.527 7.344 9.524 11.030 13.362 15.507 20.090 26.124
9 3.325 4.168 5.380 6.393 8.343 10.656 12.242 14.684 16.919 21.666 27.877
10 3.940 4.865 6.179 7.267 9.342 11.781 13.442 15.987 18.307 23.209 29.588
11 4.575 5.578 6.989 8.148 10.341 12.899 14.631 17.275 19.675 24.725 31.264
12 5.226 6.304 7.807 9.034 11.340 14.011 15.812 18.549 21.026 26.217 32.909
13 5.892 7.042 8.634 9.926 12.340 15.119 16.985 19.812 22.362 27.688 34.528
14 6.571 7.790 9.467 10.821 13.339 16.222 18.151 21.064 23.685 29.141 36.123
15 7.261 8.547 10.307 11.721 14.339 17.322 19.311 22.307 24.996 30.578 37.697
16 7.962 9.312 11.152 12.624 15.338 18.418 20.465 23.542 26.296 32.000 39.252
17 8.672 10.085 12.002 13.531 16.338 19.511 21.615 24.769 27.587 33.409 40.790
18 9.390 10.865 12.857 14.440 17.338 20.601 22.760 25.989 28.869 34.805 42.312
19 10.117 11.651 13.716 15.352 18.338 21.689 23.900 27.204 30.144 36.191 43.820
20 10.851 12.443 14.578 16.266 19.337 22.775 25.038 28.412 31.410 37.566 45.315
21 11.591 13.240 15.445 17.182 20.337 23.858 26.171 29.615 32.671 38.932 46.797
22 12.338 14.041 16.314 18.101 21.337 24.939 27.301 30.813 33.924 40.289 48.268
23 13.091 14.848 17.187 19.021 22.337 26.018 28.429 32.007 35.172 41.638 49.728
24 13.848 15.659 18.062 19.943 23.337 27.096 29.553 33.196 36.415 42.980 51.179
25 14.611 16.473 18.940 20.867 24.337 28.172 30.675 34.382 37.652 44.314 52.620
26 15.379 17.292 19.820 21.792 25.336 29.246 31.795 35.563 38.885 45.642 54.052
27 16.151 18.114 20.703 22.719 26.336 30.319 32.912 36.741 40.113 46.963 55.476
28 16.928 18.939 21.588 23.647 27.336 31.391 34.027 37.916 41.337 48.278 56.892
29 17.708 19.768 22.475 24.577 28.336 32.461 35.139 39.087 42.557 49.588 58.301
30 18.493 20.599 23.364 25.508 29.336 33.530 36.250 40.256 43.773 50.892 59.703

t-Verteilung: Stichprobenmittelwerte

5 Antworten

Idee

Die \(t\)-Verteilung wird insbesondere für Hypothesentests und Konfidenzintervalle benötigt. In beiden Situationen interessiert uns nämlich die Verteilung des Stichprobenmittelwerts.

Und falls die wahre Varianz \(\sigma^2\) der Daten nicht bekannt ist, d.h. man stattdessen die Stichprobenvarianz \(s^2\) berechnen muss (und das ist in der Realität quasi immer so), ist der Mittelwert der Stichprobe nämlich nicht normalverteilt, sondern \(t\)-verteilt mit \(n-1\) Freiheitsgraden.

Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Wenn ich also aus einer großen Grundgesamtheit (mit Mittelwert 0) für 365 Tage lang jeden Tag eine Stichprobe der Größe \(n=30\) ziehe, und dann den Mittelwert daraus bilde, folgen die so bestimmten 365 Mittelwerte einer \(t\)-Verteilung mit \(n-1=29\) Freiheitsgraden. Das Histogramm dieser 365 Datenpunkte läge also sehr nah an dieser theoretischen \(t\)-Verteilung der Daten.

Es gilt dann:

\[ \begin{align*} T &= \frac{\bar{X} – \mu_0}{s} \sqrt{n} \\ T & \sim t(n-1) \end{align*} \]

Die Standardisierung, d.h. das Subtrahieren von \(\mu_0\) und das Teilen durch \(s\), geschieht aus dem Grund, dass die danach erhaltenen Zahlen auf einer einheitlichen Skala leben (man kann sagen: von etwa -3 bis +3), und man dann nur eine einzige Tabelle drucken muss. Wenn man zum Beispiel mit einem Hypothesentest überprüfen möchte, ob die durchschnittliche Körpergrösse bei Männern 175cm ist, dann setzt man \(\mu_0 = 175\). Vom tatsächlichen durchschnittlichen Wert der Stichprobe (z.B. 176.3cm) zieht man nun die postulierten 175cm (also \(\mu_0\)) ab, und teilt durch die berechnete Standardabweichung \(s\) aus der Stichprobe.

Als kurze Anmerkung sei erwähnt, dass für größere Stichproben (Faustregeln sprechen oft von \(n>50\) oder \(df>50\)) statt der \(t\)-Verteilung als Approximation auch die Normalverteilung verwendet werden kann. Die Kurven der Dichte und Verteilungsfunktion der Normalverteilung und \(t\)-Verteilung mit sehr vielen Freiheitsgraden sind nämlich ähnlich genug, dass es fast keinen Unterschied macht, welche man verwendet.

Parameter

Je größer die Stichprobe wird, desto größer wird die Anzahl der Freiheitsgrade, und desto mehr ähnelt die zugehörige \(t\)-Verteilung dann der Normalverteilung. Die folgende Grafik veranschaulicht den Einfluss des Parameters \(df\):

a

Die \(t\)-Verteilung hat eine breitere Streuung als die Standardnormalverteilung \(N(0,1)\). Mit steigender Anzahl der Freiheitsgrade \(df\) nähert sich die \(t\)-Verteilung aber der Normalverteilungskurve an. Ab etwa \(df=50\) ist sie nah genug an der Normalverteilung, dass man die \(t\)-Verteilung mit ihr approximieren kann.

Je höher also die Anzahl der Freiheitsgrade \(df\), desto ähnlicher ist die \(t\)-Verteilung der Standardnormalverteilung \(N(0,1)\). Ab etwa 50 Freiheitsgraden, also \(df>50\), kann man mit dem Auge fast keinen Unterschied mehr zwischen den beiden Kurven erkennen.

Für eine \(t\)-verteilte Zufallsvariable \(X\) mit \(df\) Freiheitsgraden schreibt man

\[ X \sim t(df) \]

Träger

Die \(t\)-Verteilung geht genauso wie die Normalverteilung über die gesamten reellen Zahlen. Ihr Träger ist also

\[ \mathcal{T} = \mathbb{R} \]

Erwartungswert, Varianz und Dichte

Man benötigt in der Praxis eigentlich nur die Verteilungsfunktion der \(t\)-Verteilung, wie vorher schon erwähnt, um Hypothesentests und Konfidenzintervalle rechnen zu können. Es wird also in der Statistik (und in Klausuren) in den allermeisten Fällen weder die Dichtefunktion, noch Erwartungswert und Varianz vorkommen.

Der Vollständigkeit halber sei aber erwähnt, dass für eine \(t\)-verteilte Zufallsvariable der Erwartungswert \(\mathbb{E}(X) = 0\), und die Varianz \(\mathbb{V}(X) = \frac{df}{df-2}\) ist.

Verteilungsfunktion

Die Verteilungsfunktion (genauso wie die Dichtefunktion) lässt sich nur sehr eklig als Formel notieren. Das Ausrechnen dieser Funktion ist wohl niemandem zuzumuten, weshalb es für die \(t\)-Verteilung auch eine Verteilungstabelle gibt, in der man die wichtigsten Werte nachschlagen kann.

f

Verteilungsfunktionen für drei ausgewählte \(t\)-Verteilungen. Auch die Verteilungsfunktion ähnelt sich mit steigenden Freiheitsgraden immer mehr der Standardnormalverteilung an.

 

Tabelle t-Verteilung

2 Antworten

Der Unterschied der \(t\)-Verteilung zur Standardnormalverteilung ist, dass es viele verschiedene \(t\)-Verteilungen gibt – eine für jeden Freiheitsgrad \(df\).

Daher findet man aus Platzgründen in Büchern und Klausuren nie eine seitenlange Auflistung von je einer vollständigen Verteilungstabelle für jeden Freiheitsgrad, sondern nur die wichtigsten Quantile in einer Spalte.

Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Die verbreitete Schreibweise ist für ein t-Quantil dann z.B. \(t_{0.975}(4)\). Das ist das 97,5%-Quantil der t-Verteilung mit 4 Freiheitsgraden. Für dieses Quantil sind die folgenden Aussagen alle wahr und gleichbedeutend:

  • 2,5% der Fläche der Dichte der \(t\)-Verteilung mit 4 Freiheitsgraden (ab jetzt \(t(4)\)-Verteilung genannt) liegen rechts von 2,776.
  • 2,5% der Fläche der Dichte der \(t(4)\)-Verteilung liegen links von -2,776.
  • 95% der Fläche der Dichte der \(t(4)\)-Verteilung liegen im Intervall [-2,776; 2,776].
  • Eine \(t(4)\)-verteilte Zufallsvariable wird mit 95% Wahrscheinlichkeit im Intervall [-2,776; 2,776] liegen.
  • Das 97,5%-Quantil der \(t(4)\)-Verteilung ist 2,776.

Die folgende Grafik visualisiert diese 2,776.

a

So interpretiert man die aus der Verteilungstabelle abgelesenen Quantile.

Versuche zur Übung, den Wert 2,776 in der unten stehenden Verteilungstabelle wiederzufinden! Du brauchst das 97,5%-Quantil (also das 0.975-Quantil) der t-Verteilung mit 4 Freiheitsgraden!

Wenn man versteht, dass all diese Sätze äquivalent sind, dann kann man gut mit der Verteilungstabelle umgehen. Die Zeit dafür zu investieren, zahlt sich in der Klausur mit Sicherheit aus.

Anzahl Freiheitsgrade (\(df\)) Entsprechende Irrtumswahrscheinlichkeit \(\alpha\) bei zweiseitigem Test
0,5 0,25 0,2 0,1 0,05 0,02 0,01 0,002
Quantil der \(t\)-Verteilung
0,75 0,875 0,90 0,95 0,975 0,99 0,995 0,999
1 1,000 2,414 3,078 6,314 12,706 31,821 63,657 318,309
2 0,816 1,604 1,886 2,920 4,303 6,965 9,925 22,327
3 0,765 1,423 1,638 2,353 3,182 4,541 5,841 10,215
4 0,741 1,344 1,533 2,132 2,776 3,747 4,604 7,173
5 0,727 1,301 1,476 2,015 2,571 3,365 4,032 5,893
6 0,718 1,273 1,440 1,943 2,447 3,143 3,707 5,208
7 0,711 1,254 1,415 1,895 2,365 2,998 3,499 4,785
8 0,706 1,240 1,397 1,860 2,306 2,896 3,355 4,501
9 0,703 1,230 1,383 1,833 2,262 2,821 3,250 4,297
10 0,700 1,221 1,372 1,812 2,228 2,764 3,169 4,144
11 0,697 1,214 1,363 1,796 2,201 2,718 3,106 4,025
12 0,695 1,209 1,356 1,782 2,179 2,681 3,055 3,930
13 0,694 1,204 1,350 1,771 2,160 2,650 3,012 3,852
14 0,692 1,200 1,345 1,761 2,145 2,624 2,977 3,787
15 0,691 1,197 1,341 1,753 2,131 2,602 2,947 3,733
16 0,690 1,194 1,337 1,746 2,120 2,583 2,921 3,686
17 0,689 1,191 1,333 1,740 2,110 2,567 2,898 3,646
18 0,688 1,189 1,330 1,734 2,101 2,552 2,878 3,610
19 0,688 1,187 1,328 1,729 2,093 2,539 2,861 3,579
20 0,687 1,185 1,325 1,725 2,086 2,528 2,845 3,552
21 0,686 1,183 1,323 1,721 2,080 2,518 2,831 3,527
22 0,686 1,182 1,321 1,717 2,074 2,508 2,819 3,505
23 0,685 1,180 1,319 1,714 2,069 2,500 2,807 3,485
24 0,685 1,179 1,318 1,711 2,064 2,492 2,797 3,467
25 0,684 1,178 1,316 1,708 2,060 2,485 2,787 3,450
26 0,684 1,177 1,315 1,706 2,056 2,479 2,779 3,435
27 0,684 1,176 1,314 1,703 2,052 2,473 2,771 3,421
28 0,683 1,175 1,313 1,701 2,048 2,467 2,763 3,408
29 0,683 1,174 1,311 1,699 2,045 2,462 2,756 3,396
30 0,683 1,173 1,310 1,697 2,042 2,457 2,750 3,385
40 0,681 1,167 1,303 1,684 2,021 2,423 2,704 3,307
50 0,679 1,164 1,299 1,676 2,009 2,403 2,678 3,261
\(\infty\) 0,674 1,150 1,282 1,645 1,960 2,326 2,576 3,090

Normalverteilung: Körpergrösse

16 Antworten

Idee

Die Normalverteilung ist aus vielen Gründen die wichtigste Verteilung in der Statistik:

  • Modelle (zum Beispiel das lineare Regressionsmodell) mit Normalverteilung sind besonders einfach zu rechnen, da die Formeln zur Bestimmung der Parameter \(\beta\) im Normalverteilungsfall sehr leicht auszuwerten sind.
  • Der Durchschnitt einer Stichprobe mit beliebiger Verteilung folgt einer Normalverteilung. Das ist weitaus wichtiger als es beim ersten Mal lesen klingt. Ich kann 100 Zufallszahlen aus irgendeiner Verteilung (stetig oder diskret, auch selbstgebastelte Verteilungen mit irgendeiner Dichte) ziehen, und ihr Mittelwert folgt immer einer Normalverteilung. Dieses Phänomen ist als zentraler Grenzwertsatz bekannt, und wird z.B. beim klassischen \(t\)-Test wichtig. Dort bildet man nämlich einen Stichprobenmittelwert und nutzt aus, dass er annähernd normalverteilt ist.
  • Viele natürliche Merkmale folgen einer Normalverteilung. Besonders wenn es ein Merkmal ist, dass aus dem Durchschnitt vieler einzelner Eigenschaften gebildet wird, ist das Resultat am Ende zumindest annähernd normalverteilt. Die Körpergrösse einer Person ist zum Beispiel das Ergebnis (der „Durchschnitt“) vieler verschiedener genetischen Faktoren, und kann für ein gegebenes Geschlecht auch sehr gut mit einer Normalverteilung modelliert werden.
Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Parameter

Die Glockenkurve der Normalverteilung ist abhängig von zwei Parametern: Dem Mittelwert \(\mu\) und der Varianz \(\sigma^2\). Man notiert eine normalverteilte Zufallsvariable \(X\) als

\[ X \sim \text{N}(\mu, \sigma^2) \]

Mit dem Mittelwert \(\mu\) verschiebt man die Kurve nach links bzw. rechts, und mit der Varianz \(\sigma^2\) verändert man die Form der Kurve – also ob sie enger oder weiter ist. Das folgende Bild veranschaulicht den Einfluss der Parameter:

Verschiedene Normalverteilungen

Der Einfluss der Parameter \(\mu\) und \(\sigma^2\) auf die Dichte der Normalverteilung.

Vorsicht: Der Parameter ist meist die Varianz, also \(\sigma^2\). Beim Rechnen mit der Normalverteilung (zum Beispiel beim Standardisieren der Zufallsvariablen oder bei Hypothesentests) wird oft mit der Standardabweichung \(\sigma\), also der Wurzel der Varianz, gearbeitet. Hier muss man immer genau hinschauen, welche Variante verwendet wird, und gegebenenfalls zwischen den beiden Werten umrechnen.

Träger

Bei jeder Normalverteilung, also egal welche Parameter \(\mu\) und \(\sigma^2\) sie hat, sind theoretisch alle Realisationen aus den positiven und negativen reellen Zahlen möglich. Der Träger einer Normalverteilung ist also

\[ \mathcal{T} = \mathbb{R} \]

Das erscheint vielleicht etwas seltsam, da man die Normalverteilung oft auch dazu verwendet, Dinge wie die Körpergrösse zu modellieren, und es kann ja keine negativen Körpergrössen geben. Man sollte aber zwei Dinge beachten:

  • Bei der Modellierung der Körpergrösse wird zum Beispiel eine Normalverteilung mit \(\mu=165\)cm und \(\sigma^2=100\) verwendet. Da liegt die Wahrscheinlichkeit, dass eine Realisation kleiner als 0 herauskommt, bei ungefähr \(2\cdot 10^{-61}\). Diese Zahl ist eine Null, ein Komma, 60 Nullen, und dann erst eine zwei. Das ist so vernachlässigbar klein, dass in der gesamten Geschichte der Menschheit keine Person in diesem Bereich erwartet wird.
  • Die Normalverteilung ist natürlich nur ein „gut genug“ passendes Modell, das zur Beschreibung der Körpergrösse verwendet wird. Die wahre Verteilung der Körpergrösse von Menschen sieht anders aus (und hat natürlich nur einen positiven Träger), aber niemand kennt diese Verteilung, und sie lässt sich wohl auch nicht durch eine so einfache Formel hinschreiben. Daher verwendet man bekannte Verteilungen als Approximation. Man sagt, dass eine bestimmte Verteilung gut genug zur Modellierung ist, und nimmt solche, mit denen man besonders einfach rechnen kann.

Erwartungswert

Der Erwartungswert ist direkt der erste Parameter, \(\mu\). Bei einer Normalverteilung mit \(\mu=4\) erwartet man also im Durchschnitt eine Realisation von 4, egal wie groß die Varianz \(\sigma^2\) ist.

Varianz

Die Varianz der Normalverteilung ist der zweite Parameter, \(\sigma^2\). In der Hinsicht ist die Normalverteilung ein Sonderfall, da ihre beiden Parameter direkt der Erwartungswert und die Varianz sind – sehr bequem.

Dichte

Die Dichtefunktion einer normalverteilten Zufallsvariablen \(X\) mit Parametern \(\mu\) und \(\sigma^2\) lautet

\[ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot \exp \left( – \frac{(x-\mu)^2}{2\sigma^2} \right) \]

Wenn man sich statt der Varianz \(\sigma^2\) die Standardabweichung \(\sigma\), also \(\sqrt{\sigma^2}\) anschaut, kann man eine beliebige Normalverteilungsdichte skizzieren. Sie hat ihr Maximum an der Stelle \(\mu\), und fällt dann im Bereich von ungefähr \(\pm 3 \sigma\) ab. Außerhalb eines Abstandes von \(3\sigma\) ist die Dichte sehr nahe bei Null.

verteilungen-normalverteilung-skizze

Skizze einer Normalverteilung mit \(\mu=0\) und \(\sigma^2=1\).

Verteilungsfunktion

Die Verteilungsfunktion der Normalverteilung kann man nicht mit einer Formel im Taschenrechner berechnen. Das Integral über die Dichtefunktion lässt sich nämlich nicht mit Stift und Papier lösen:

\[ F(x) = \int_{-\infty}^t \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( – \frac{(t-\mu)^2}{2\sigma^2} \right) dt \]

Man nimmt daher eine Verteilungstabelle her, die man häufig am Ende von Statistikbüchern, oder in der Anlage zu Klausuren findet. Wie man die abliest, wird im entsprechenden Artikel erklärt.

a

Verteilungsfunktion \(\Phi(z)\) der Standardnormalverteilung (also mit \(\mu=0\) und \(\sigma^2=1\)).

Zum Ablesen von Verteilungstabellen

Nun hat man das Problem, dass es unendlich viele Normalverteilungen gibt, mit jeweils unterschiedlichen Parametern \(\mu\) und \(\sigma^2\). Man bräuchte also eine Tabelle für die Verteilung \(\text{N}(10, 1)\), eine für \(\text{N}(10, 1.4)\), und so weiter. Man hilft sich hier dadurch, indem man nur eine Tabelle verwendet, und zwar für die Standardnormalverteilung, also \(X\sim \text{N}(0,1)\), mit \(\mu=0\) und \(\sigma^2=1\). Nun kann man eine beliebige Normalverteilung standardisieren, und dann deren Wert anhand der Verteilungstabelle bestimmen.

Standardisieren von normalverteilten Zufallsvariablen

Angenommen, wir haben eine Zufallsvariable \(X\sim \text{N}(4, 1)\), und möchten ihre Verteilungsfunktion an der Stelle \(x=3\) wissen. Wir suchen also die Wahrscheinlichkeit, dass diese Zufallsvariable einen Wert kleiner oder gleich 3 erhält. Man muss sich jetzt klar darüber werden, dass das genau dasselbe ist, wie wenn ich für eine Zufallsvariable \(Z\sim \text{N}(0,1)\) die Verteilungsfunktion an der Stelle \(x=-1\) suche. Das folgende Bild veranschaulicht die Gleichheit der beiden Werte anhand der Fläche unter der Dichte:

Die linke Fläche, d.h. \(\mathbb{P}(X \leq 3)\) für die Zufallsvariable \(X\sim \text{N}(4, 1)\) ist genau gleich der Fläche \(\mathbb{P}(Z \leq -1)\) für die Standardnormalverteilung \(Z\sim \text{N}(0,1)\).

Man standardisiert eine normalverteilte Zufallsvariable \(X\), indem man also, wie gerade gezeigt, zuerst ihren Mittelwert abzieht, und danach durch die Standardabweichung teilt:

\[ Z = \frac{X-\mu}{\sigma} \]

Das Teilen durch die Standardabweichung streckt bzw. staucht die Glockenkurve so, dass danach ihre Varianz gleich 1 ist.

Damit kann man nun die Verteilungsfunktion jeder beliebigen Normalverteilung bestimmen.

Es gilt also:

\[ \mathbb{P}(X \leq x) = \mathbb{P}(Z \leq \frac{x-\mu}{\sigma}) = \Phi(\frac{x-\mu}{\sigma}) = \Phi(z) \]

Die Standardnormalverteilung wird dabei statt \(F(x)\) mit \(\Phi(z)\) notiert, um Verwechslungen mit der unstandardisierten Verteilungsfunktion zu vermeiden.

Damit können wir nun den oben gesuchten Wert \(\mathbb{P}(X \leq 3)\) für die Zufallsvariable \(X\sim \text{N}(4,1)\) bestimmen:

\[ \mathbb{P}(X \leq 3) = \mathbb{P}(Z \leq \frac{3-4}{1}) = \mathbb{P}(Z \leq -1) = \Phi(-1) = 1 -\Phi(1) = 1 – 0.8413 = 0.1587 \]

Den Wert 0.8413 haben wir dabei mit der Verteilungstabelle bestimmt. Wir mussten die Umrechnung \(\mathbb{P}(Z \leq -1) = 1 -\mathbb{P}(Z \leq 1)\) einführen, da in der Tabelle nur die positiven Werte tabelliert sind. Die Details dazu sind im Artikel zur Verteilungstabelle erklärt.

Der Wert \(F(3)\) der Zufallsvariablen \(X\) ist also gleich dem Wert \(\Phi(-1)\) der standardisierten Zufallsvariable \(Z\). Und da \(\Phi(-1)\) nicht in der Tabelle steht, formen wir es noch um in \(1-\Phi(1)\), und schlagen den Wert für \(\Phi(1)\) nach.

Aufgaben zum Standardisieren

Das Standardisieren muss man einfach einige Male drillen, dann hat man das Prinzip verinnerlicht und Leichtsinnsfehler beseitigt. Bestimme zur Übung die folgenden Werte für verschiedene Normalverteilungen. Beachte, dass der zweite Parameter, \(\sigma^2\), zum Standardisieren noch in die Standardabweichung transformiert werden muss:

  • a) Sei \(X\sim \text{N}(2,1)\). Bestimme \(\mathbb{P}(X \leq 3)\).
  • b) Sei \(X\sim \text{N}(-1, 4)\). Bestimme \(\mathbb{P}(X \leq 0)\).
  • c) Sei \(X\sim \text{N}(0, 5)\). Bestimme \(\mathbb{P}(X > 2)\).
  • d) Sei \(X\sim \text{N}(123, 456)\). Bestimme \(\mathbb{P}(X \leq 130)\).
  • e) Sei \(X\sim \text{N}(150, 100)\). Bestimme \(\mathbb{P}(160 < X \leq 170)\).
Lösung (klick)
  • a) Wir suchen also für \(\mu=2\) und \(\sigma^2=1\) (d.h. auch \(\sigma=1\)) den Wert \(\mathbb{P}(X \leq 3)\). Der äquivalente \(z\)-Wert der Standardnormalverteilung ist \(\frac{x-\mu}{\sigma} = \frac{3-2}{1} = 1\). Es ist also
    \[ \mathbb{P}(X \leq 3) = \mathbb{P}(Z \leq 1) = 0.8413 \]
  • b) Die Standardabweichung \(\sigma\) ist hier \(\sigma=\sqrt{4}=2\). Damit ist hier \(\mathbb{P}(X \leq 0) = \mathbb{P}(Z \leq \frac{0-(-1)}{2}) = \mathbb{P}(Z \leq 0.5) = \Phi(0.5) = 0.6915\)
  • c) Vorsicht: Hier ist die Wahrscheinlichkeit gesucht, dass \(X\) größer als 2 ist. Wir bestimmen das mit der Gegenwahrscheinlichkeit, d.h. wir berechnen
    \[ \mathbb{P}(X > 2) = 1 – \mathbb{P}(X \leq 2) \] Wir bestimmen also
    \[ 1-\mathbb{P}(X \leq 2) = 1-\mathbb{P}(Z \leq \frac{2-0}{\sqrt{5}}) = 1-\mathbb{P}(Z \leq 0.894) = 1-\Phi(0.89) = 1-0.8132 = 0.1867 \]
  • d) \(\mathbb{P}(X \leq 130) = \mathbb{P}(\frac{X-123}{\sqrt{456}} \leq \frac{130-123}{\sqrt{456}}) = \mathbb{P}(Z \leq 0.33) =\Phi(0.33) = 0.6293\)
  • e) Hier brauchen wir die Differenz der Werte der Verteilungsfunktion an der Stelle \(x=170\) und an \(x=160\). Das Vorgehen ist im allgemeinen Artikel zur Verteilungsfunktion beschrieben. Wir berechnen also:
    \[ \mathbb{P}(X \leq 170) = \mathbb{P}(Z \leq \frac{170-150}{\sqrt{100}}) =\Phi(2) = 0.977 \] \[ \mathbb{P}(X \leq 160) = \mathbb{P}(Z \leq \frac{160-150}{\sqrt{100}}) =\Phi(1) = 0.841 \] Das Ergebnis ist also \(\Phi(2)-\Phi(1) = 0.136\).

Quantile bestimmen

Das \(\alpha\)-Quantil einer Normalverteilung bestimmt man genau umgekehrt wie den Wert der Verteilungsfunktion:

Man schlägt zuerst das \(\alpha\)-Quantil der Standardnormalverteilung in der Verteilungstabelle nach. Nennen wir es \(z_\alpha\). Man transformiert es nun in das Quantil \(q_\alpha\) der tatsächlichen Normalverteilung, indem man es erst mit \(\sigma\) multipliziert, und dann noch \(\mu\) addiert. Es ist also

\[ q_\alpha = \mu + \sigma \cdot z_\alpha \]

Aufgaben zum Bestimmen von Quantilen

  • a) Sei \(X\sim \text{N}(2,1)\). Bestimme das 75%-Quantil \(q_{0.75}\).
  • b) Sei \(X\sim \text{N}(-1, 4)\). Bestimme das 50%-Quantil \(q_{0.5}\).
  • c) Sei \(X\sim \text{N}(0, 5)\). Bestimme das 97.5%-Quantil \(q_{0.975}\).
  • d) Sei \(X\sim \text{N}(123, 456)\). Bestimme das 2.5%-Quantil \(q_{0.025}\).
  • e) Sei \(X\sim \text{N}(150, 100)\). Bestimme das 10%-Quantil \(q_{0.1}\).
Lösung (klick)
  • a) Das 75%-Quantil der Standardnormalverteilung ist \(z_{0.75}=0.67\). Wir übersetzen das in das 75%-Quantil der \(\text{N}(2,1)\)-Verteilung:
    \[ q_{0.75} = \mu + \sigma z_{0.75} = 2 + 1 \cdot 0.67 = 2.67\]
  • b) \(q_{0.5} = \mu + \sigma z_{0.5} = -1 + \sqrt{4} \cdot 0 = -1\). Das 50%-Quantil (d.h. der Median) jeder Normalverteilung ist automatisch ihr Mittelwert \(\mu\).
  • c) \(q_{0.975} = \mu + \sigma z_{0.975} = 0 + \sqrt{5} \cdot 1.96 = 4.382\)
  • d) Das 2.5%-Quantil der Standardnormalverteilung ist \(z_{0.025} = -z_{0.975} = -1.96\). Damit ist \(q_{0.025} = \mu + \sigma z_{0.025} = 123 + \sqrt{456} \cdot (-1.96) = 81.15\)
  • e) \(q_{0.1} =\mu + \sigma z_{0.1} = 150 + \sqrt{100} \cdot (-z_{0.9}) = 150 + 10 \cdot (-1.28) = 137.2\)

Tabelle Normalverteilung

6 Antworten

Wie man die Verteilungstabelle abliest

Weil die Standardnormalverteilung so eine zentrale Rolle spielt (und, damit man sie nicht mit der Verteilungsfunktion von unstandardisierten Zufallsvariablen verwechselt), bekommt diese Verteilung meist einen eigenen Buchstaben, das griechische grosse Phi. Statt \(F(x)\) schreibt man in den meisten Büchern und Vorlesungen dann \(\Phi(z)\), wobei \(z\) für den standardisierten Wert steht.

Klausuraufgaben
Im eBook-Shop gibt es Klausuraufgaben zu diesem Thema!
Zu den eBooks

Um Platz zu sparen, ist in den meisten Büchern und Klausuren nur die rechte Hälfte der Verteilungsfunktion tabelliert.

aa

Die Verteilungsfunktion der Normalverteilung. In Tabellen findet man häufig nur die rechte Hälfte dieser Kurve, also ab \(\Phi(0)=0.5\).

Den Wert \(\Phi(z)\) für alle positiven \(z\) kann man nun einfach aus der Tabelle ablesen. Meistens sind die Tabellen so aufgebaut, dass in den Zeilen die ersten beiden Stellen für \(z\) stehen, und in 10 Spalten dann die zweite Nachkommastelle. Aus der Tabelle liest man also z.B. \(\Phi(0.01) = 0.5040\), oder \(\Phi(1.96) = 0.975\).

Um den Wert \(\Phi(z)\) für ein negatives \(z\), zum Beispiel \(\Phi(-1.5)\) zu erhalten, ist dann ein zusätzlicher Rechenschritt nötig, der in der folgenden Grafik erklärt ist.

s

So berechnet man die Verteilungsfunktion an negativen \(x\)-Stellen. Die beiden vertikalen Balken sind genau gleich hoch (nämlich \(\Phi(1.5)=0.93\)).

Da die Verteilungskurve nämlich symmetrisch um den Punkt (0, 0.5) ist, kann man sich dieses Tricks bedienen:

\[\Phi(-z) = 1-\Phi(z) \]

Man berechnet also die Verteilungsfunktion an der Stelle \(-1.5\), indem man den Wert für \(+1.5\) in der Tabelle findet, und ihn von 1 abzieht:

\[\Phi(-1.5) = 1-\Phi(1.5) = 1-0.933 = 0.067 \]

Zwischenaufgabe

Bestimme mit Hilfe der untenstehenden Tabelle \(\Phi(1)\), \(\Phi(-1)\), und \(\Phi(-1.96)\).

Lösung (klick)
  • \(\Phi(1)=0.8413\)
  • \(\Phi(-1) = 1-\Phi(1) = 1-0.8413 = 0.1587\)
  • \(\Phi(-1.96) = 1-\Phi(1.96) = 1-0.975 = 0.025\)

Sehr große Zahlen

Für Zahlen, die so groß (oder so klein im Negativen) sind, dass man sie nicht mehr in der Tabelle findet, kann man näherungsweise als Wahrscheinlichkeit „fast Null“ oder „fast Eins“ nehmen. An der Grafik der Verteilung oben kann man intuitiv verstehen, warum das so ist. Die Funktion nähert sich für sehr große Zahlen der 1 an, und für sehr kleine Zahlen der 0.

Als Formel ausgedrückt, falls man z.B: \(\Phi(15)\) berechnen will:

\[\Phi(15) \approx 1\]

\[\Phi(-15) \approx 0\]

Quantile ablesen

Quantile liest man genau andersherum aus der Verteilungstabelle ab, da die Quantilsfunktion ja genau die Umkehrfunktion der Verteilungsfunktion ist.

Wenn man direkt die ersten beiden Zellen der Tabelle betrachtet, ist also das 0.5000-Quantil der Standardnormalverteilung gleich 0.00. Das 0.5040-Quantil ist 0.01, und so weiter. Das 75%-Quantil liegt zwischen 0.67 und 0.68, da \(\Phi(0.67)=0.7486\) ist, und \(\Phi(0.68)=0.7517\).

Für die Quantile unter 50% muss man wieder über einen kurzen Umweg rechnen, da die Tabelle nur positive \(z\), und damit Quantile über 0.5 abbildet.

Für das \(\alpha\)-Quantil gilt: \(q_\alpha = -q_{1-\alpha}\). Das bedeutet: Möchte man das 20%-Quantil bestimmen, sucht man (weil es unter 50% liegt) in der Verteilungstabelle stattdessen das (1-0.2)-Quantil, also das 80%-Quantil, und nimmt den negativen Wert des Ergebnisses. Das 80%-Quantil ist also 0.84, und das 20%-Quantil ist somit -0.84.

Zwischenaufgabe

Bestimme das 97.5%-Quantil sowie das 2.5%-Quantil der Standardnormalverteilung.

Lösung (klick)

Die Verteilungsfunktion hat an der Stelle \(z=1.96\) den Wert \(\Phi(1.96)=0.975\). Daher ist das 97.5%-Quantil gleich 1.96.

Das 2.5%-Quantil (nennen wir es \(q_{0.025}\) ist nun \(-q_{1-0.025} = -q_{0.975}\), also -1.96.

Die Tabelle der Standardnormalverteilung

\(\downarrow\) z-Werte Zweite Nachkommastelle \(\rightarrow\)
0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,5000 0,5040 0,5080 0,5120 0,5160 0,5199 0,5239 0,5279 0,5319 0,5359
0,1 0,5398 0,5438 0,5478 0,5517 0,5557 0,5596 0,5636 0,5675 0,5714 0,5753
0,2 0,5793 0,5832 0,5871 0,5910 0,5948 0,5987 0,6026 0,6064 0,6103 0,6141
0,3 0,6179 0,6217 0,6255 0,6293 0,6331 0,6368 0,6406 0,6443 0,6480 0,6517
0,4 0,6554 0,6591 0,6628 0,6664 0,6700 0,6736 0,6772 0,6808 0,6844 0,6879
0,5 0,6915 0,6950 0,6985 0,7019 0,7054 0,7088 0,7123 0,7157 0,7190 0,7224
0,6 0,7257 0,7291 0,7324 0,7357 0,7389 0,7422 0,7454 0,7486 0,7517 0,7549
0,7 0,7580 0,7611 0,7642 0,7673 0,7703 0,7734 0,7764 0,7794 0,7823 0,7852
0,8 0,7881 0,7910 0,7939 0,7967 0,7995 0,8023 0,8051 0,8078 0,8106 0,8133
0,9 0,8159 0,8186 0,8212 0,8238 0,8264 0,8289 0,8315 0,8340 0,8365 0,8389
1,0 0,8413 0,8438 0,8461 0,8485 0,8508 0,8531 0,8554 0,8577 0,8599 0,8621
1,1 0,8643 0,8665 0,8686 0,8708 0,8729 0,8749 0,8770 0,8790 0,8810 0,8830
1,2 0,8849 0,8869 0,8888 0,8907 0,8925 0,8944 0,8962 0,8980 0,8997 0,9015
1,3 0,9032 0,9049 0,9066 0,9082 0,9099 0,9115 0,9131 0,9147 0,9162 0,9177
1,4 0,9192 0,9207 0,9222 0,9236 0,9251 0,9265 0,9279 0,9292 0,9306 0,9319
1,5 0,9332 0,9345 0,9357 0,9370 0,9382 0,9394 0,9406 0,9418 0,9429 0,9441
1,6 0,9452 0,9463 0,9474 0,9484 0,9495 0,9505 0,9515 0,9525 0,9535 0,9545
1,7 0,9554 0,9564 0,9573 0,9582 0,9591 0,9599 0,9608 0,9616 0,9625 0,9633
1,8 0,9641 0,9649 0,9656 0,9664 0,9671 0,9678 0,9686 0,9693 0,9699 0,9706
1,9 0,9713 0,9719 0,9726 0,9732 0,9738 0,9744 0,9750 0,9756 0,9761 0,9767
2,0 0,9772 0,9778 0,9783 0,9788 0,9793 0,9798 0,9803 0,9808 0,9812 0,9817
2,1 0,9821 0,9826 0,9830 0,9834 0,9838 0,9842 0,9846 0,9850 0,9854 0,9857
2,2 0,9861 0,9864 0,9868 0,9871 0,9875 0,9878 0,9881 0,9884 0,9887 0,9890
2,3 0,9893 0,9896 0,9898 0,9901 0,9904 0,9906 0,9909 0,9911 0,9913 0,9916
2,4 0,9918 0,9920 0,9922 0,9925 0,9927 0,9929 0,9931 0,9932 0,9934 0,9936
2,5 0,9938 0,9940 0,9941 0,9943 0,9945 0,9946 0,9948 0,9949 0,9951 0,9952
2,6 0,9953 0,9955 0,9956 0,9957 0,9959 0,9960 0,9961 0,9962 0,9963 0,9964
2,7 0,9965 0,9966 0,9967 0,9968 0,9969 0,9970 0,9971 0,9972 0,9973 0,9974
2,8 0,9974 0,9975 0,9976 0,9977 0,9977 0,9978 0,9979 0,9979 0,9980 0,9981
2,9 0,9981 0,9982 0,9982 0,9983 0,9984 0,9984 0,9985 0,9985 0,9986 0,9986